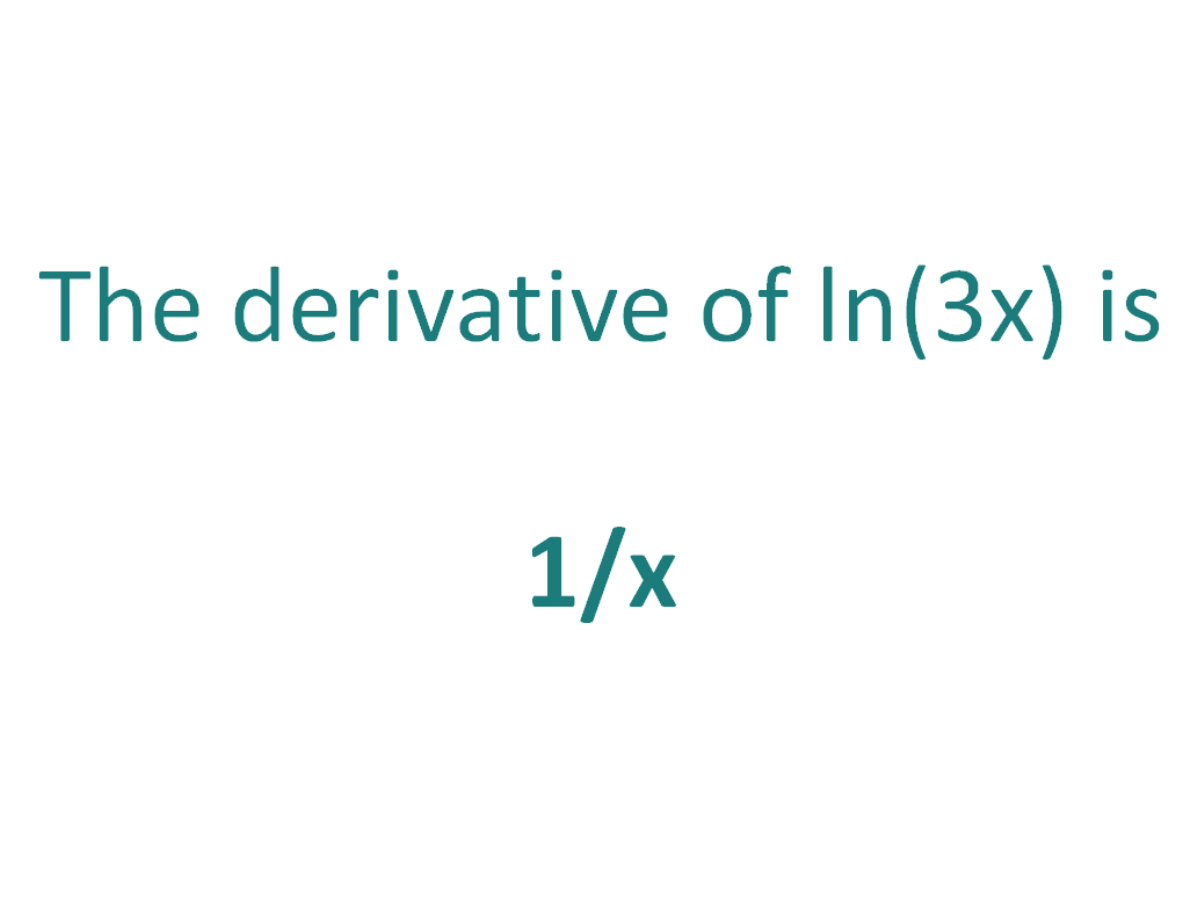The derivative of ln(3x) is 1/x
How to calculate the derivative of ln(3x)
There are two methods that can be used for calculating the derivative of ln(3x).
The first method is by using the chain rule for derivatives.
The second method is by using the properties of logs to write ln(3x) into a form which differentiable without needing to use the chain rule.
Finding the derivative of ln(3x) using the chain rule
The chain rule is useful for finding the derivative of an expression which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.
In this case:
- We know how to differentiate 3x (the answer is 3)
- We know how to differentiate ln(x) (the answer is 1/x)
This means the chain rule will allow us to perform the differentiation of the function ln(3x).
To perform the differentiation, the chain rule says we must differentiate the expression as if it were just in terms of x as long as we then multiply that result by the derivative of what the expression was actually in terms of (in this case the derivative of 3x).
Using the chain rule to find the derivative of ln(3x)
ln(3x) is in the form of the standard natural log function ln(x), except it does not have x as an argument, instead it has another function of x (3x).
Let’s call the function in the argument g(x), which means:
g(x) = 3x
From this it follows that:
ln(3x) = ln(g(x))
So if the function f(x) = ln(x) and the function g(x) = 3x, then the function ln(3x) can be written as a composite function.
f(x) = ln(x)
f(g(x)) = ln(g(x)) (but g(x) = 3x)
f(g(x)) = ln(3x)
Let’s define this composite function as F(x):
F(x) = f(g(x)) = ln(3x)
We can find the derivative of ln(3x) (F'(x)) by making use of the chain rule.
The Chain Rule:
For two differentiable functions f(x) and g(x)
If F(x) = f(g(x))
Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)
Now we can just plug f(x) and g(x) into the chain rule.
Now we can just plug f(x) and g(x) into the chain rule. But before we do that, just a quick recap on the derivative of the natural logarithm.
The derivative of ln(x) with respect to x is (1/x)
The derivative of ln(s) with respect to s is (1/s)
In a similar way, the derivative of ln(3x) with respect to 3x is (1/3x).
We will use this fact as part of the chain rule to find the derivative of ln(3x) with respect to x.
How to find the derivative of ln(3x) using the Chain Rule:
| F'(x) | = f'(g(x)).g'(x) | Chain Rule Definition |
| = f'(g(x)).(3) | g(x) = 3x ⇒ g'(x) = 3 | |
| = (1/3x).3 | f(g(x)) = ln(3x) ⇒ f'(g(x)) = 1/3x (The derivative of ln(3x) with respect to 3x is (1/3x)) | |
| = 1/x |
Using the chain rule, we find that the derivative of ln(3x) is 1/x
Finally, just a note on syntax and notation: ln(3x) is sometimes written in the forms below (with the derivative as per the calculations above). Just be aware that not all of the forms below are mathematically correct.
| ln3x | ► Derivative of ln3x =1/x |
| ln 3x | ► Derivative of ln 3x = 1/x |
| ln 3 x | ► Derivative of ln 3 x = 1/x |
Top Tip
It’s possible to generalize the derivative of expressions in the form ln(ax) (where a is a constant value):
The derivative of ln(ax) = 1/x
(Regardless of the value of the constant, the derivative of ln(ax) is always 1/x)
Finding the derivative of ln(3x) using log properties
Since ln is the natural logarithm, the usual properties of logs apply.
The product property of logs states that ln(xy) = ln(x) + ln(y). In other words taking the log of a product is equal to the summing the logs of each term of the product.
Since 3x is the product of 3 and x, we can use the product properties of logs to rewrite ln(3x):
f(x) = ln(3x) = ln(3) + ln(x)
How to find the derivative of ln(3x) using the product property of logs
| f(x) | = ln(3) + ln(x) | |
| f'(x) | = 0 + ln(x) | ln3 is a constant, the derivative of a constant is 0 |
| = 0 + 1/x | The derivative of ln(x) is 1/x | |
| = 1/x |
The Second Derivative of ln(3x)
To calculate the second derivative of a function, you just differentiate the first derivative.
From above, we found that the first derivative of ln(3x) = 1/x. So to find the second derivative of ln(3x), we just need to differentiate 1/x
If we differentiate 1/x we get an answer of (-1/x2).
► The second derivative of ln(3x) = -1/x2