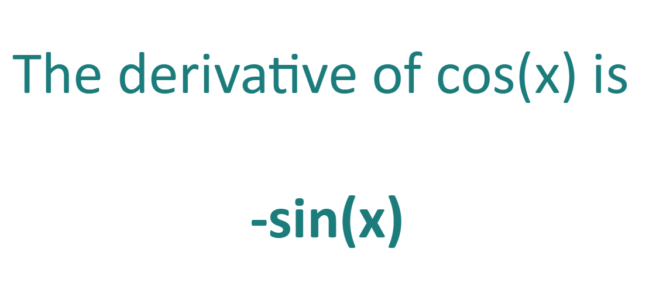What is the derivative of Cos?
In calculus, the derivative of cos(x) is equal to -sin(x)
(d/dx)cos(x) = -sin(x)
Or
cos'(x) = -sin(x)
So what does this mean and how do we get to that answer?
Well, since differentiation involves finding the rate of change (or gradient) of a function, finding the derivative of cos means that we are trying to determine the rate of change of the cos function with respect to x (the angle of the cos function).
This evaluation of the rate of change of the cos function with respect to the variable x is found to be negative sine of x (-sin(x)).
Next we will look at how we calculate the derivative of cos(x).
The derivative of cos(x) from first principles
To find the derivative of cos(x) (or in fact any function) it is often a good idea to start with first principles and the definition of the derivative of a function.
Recall that derivative of a function f(x) (or f'(x)) can be expressed as
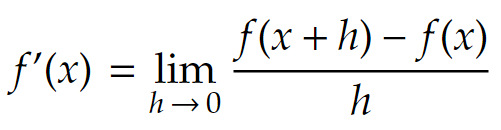
In this case f(x), the function we want to differentiate is cos(x). So if we put f(x) = cos(x) into the definition of the derivative function we get

Next, we need to use the following trigonomic identity relating to cos and the sum of two angles. You may recall (if you don’t then just accept it as fact for now)

We can then apply this trig identity to the cos(x+h) term from above to get:

Then we can do some factorisation of the numerator by rearranging it a little and taking out a common cos(x) term:

Finally, we split the numerator up so that we can apply two formulas related to finding the limits of trigonometric functions.
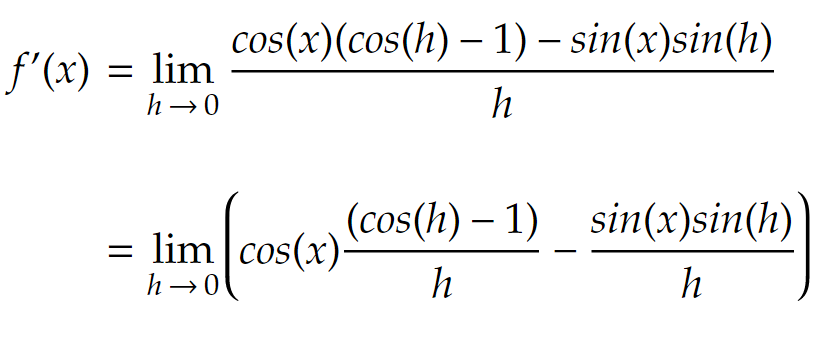
The following two formulas relating to limits of sin and cos now come in handy. We can plug these two in and then solve:

And that proves that the derivative of cos(x) is -sin(x)