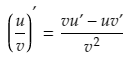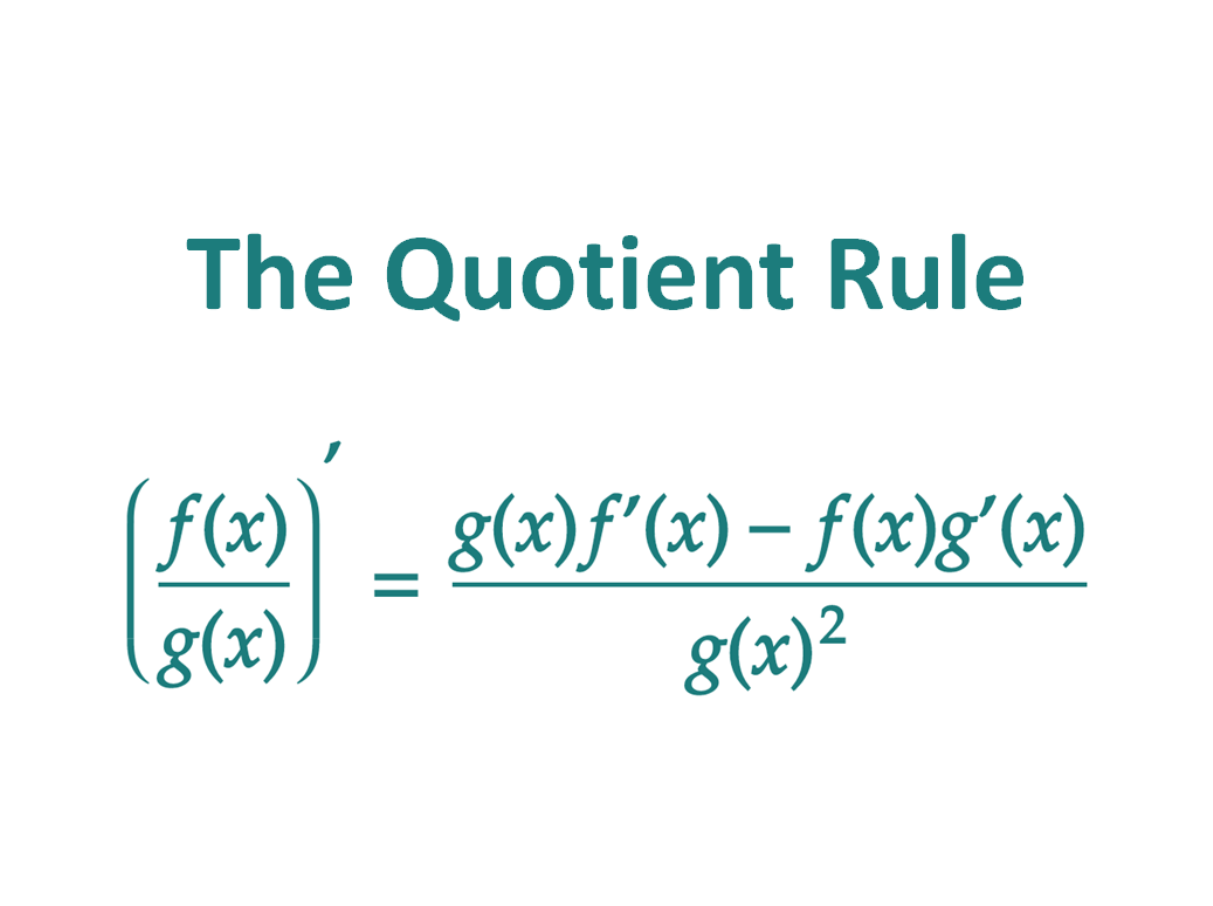In calculus, the quotient rule is used to find the derivative of a function which can be expressed as a ratio of two differentiable functions. In other words, the quotient rule allows us to differentiate functions which are in fraction form.
Say for example we had two functions:
f(x) = x2 and
g(x) = x
Now say we wanted to find the derivative of

One approach to find the derivative would be to simplify the function and then differentiate it.
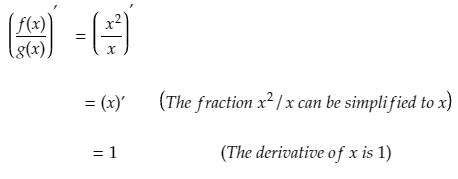
So the derivative of the fraction f(x)/g(x) is just 1.
Now, out of interest, let’s calculate f’(x)/g’(x) (by differentiating the numerator and then the denominator)
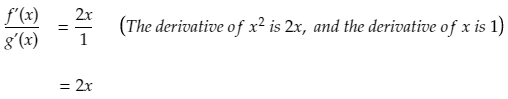
So we can see that (f(x)/g(x))’ = 1, and that is not equal to (f’(x)/g’(x)) = 2x
The derivative of a quotient is not equal to the quotient of the derivatives.
To differentiate a quotient, you cannot just take the derivative of the numerator and divide it by the derivative of the denominator. Instead, we need to use the quotient rule to find the derivative of a quotient (in a similar way that the product rule needs to be used to find the derivative of a product).
The Quotient Rule Formula For Differentiation
If two functions f(x) and g(x) are differentiable (i.e. the derivatives of f(x) and g(x) exist), then their quotient (f(x)/g(x)) is differentiable, and the derivative can be found as follows:
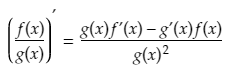
The formula for the quotient rule in words
The Quotient Rule states that the derivative of a quotient is equal to the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator.
Two tricks to remember the quotient rule
Similar to the product rule, you need to find the derivative of f(x) and then multiply it with g(x) and then find the derivative of g(x) and multiply it by f(x). However, because the terms are subtracted, the order matters, and there is also a division which needs to be performed.
This makes the quotient rule a little more difficult to memorize compared to the product rule.
Here are two methods which may help you remember the quotient rule:
1. You always start with the bottom function (denominator) and end with the bottom function squared.
And if that doesn’t work…
2. Here is a jingle which you can use:
Lo d hi minus hi d low, all over the square of what’s below.
Here the lo, refers to the denominator, hi refers to the numerator and d refers to “the derivative of”. It’s really silly, but that’s why it works!
When to use the quotient rule
In calculus, the quotient rule can be applied when the function you want to differentiate consists of a quotient (or fraction), and the numerator and denominator of the quotient are both differentiable functions of their own.
For example the function f(x) = x/x2 can be differentiated using the quotient rule for derivatives because:
- The numerator (x) is differentiable – its derivative is 1
- The denominator (x2) is differentiable – it’s derivative is x
(Of course you could also first simplify the function to 1/x and then differentiate it and get the same result)
Examples Using The Quotient Rule
The best way to see how the quotient rule works is by looking at some examples.
Using the quotient rule
For the first example, let’s find the derivative of
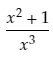
Let’s call the numerator f(x), so f(x) = x2 + 1
Let’s call the denominator g(x), so g(x) = x3
This means that:
f'(x) = 2x
g'(x) = 3x2
We can now apply the quotient rule to find the derivative of f(x)/g(x). The formula for the quotient rule is

Now we can plug f(x), f'(x), g(x) and g'(x) into the formula
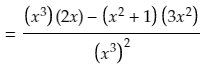
And then we just simplify using factorization and the rules of exponents to find the final answer
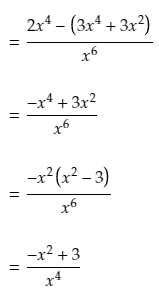
Using the quotient rule with trig functions
As another example, we can use the quotient rule to find the derivative of tan(x)
First recall that tan(x) can be expressed as sin(x) divided by cos(x)

Let’s call the numerator f(x), so f(x) = sin(x)
Let’s call the denominator g(x), so g(x) = cos(x)
This means that:
f'(x) = cos(x)
g'(x) = -sin(x)
We can now apply the quotient rule to find the derivative of f(x)/g(x). The formula for the quotient rule is
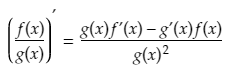
Now we can plug f(x), f'(x), g(x) and g'(x) into the formula:

Then simplify remembering the trig identity sin2(x) + cos2(x) = 1 and recalling that 1/cos(x) is equal to sec(x).

Using the quotient rule, the derivative of tan(x) is equal to sec2(x)
Proof of the Quotient Rule
There are a number of ways to prove the quotient rule. Here we will look at proving the quotient rule using:
- First principles – the derivative definition and properties of limits.
- Implicit differentiation and the product rule
- The product and chain rules
- Natural logarithms and the chain rule
Proving the quotient rule using first principles
Let F(x) = f(x)/g(x)
The definition for the derivative of F(x) is
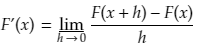
Then we put F(x+h) and F(x) in
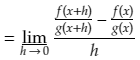
This can be rewritten by finding the lowest common denominator in the numerator (g(x+h).g(x)) and taking the 1/h out.

The next step is needed to make life easier a little later on. What we do is we add 0 to the numerator, which does not change the value at all. But instead of adding a straight 0, we add it in the form -f(x)g(x) + f(x)g(x)
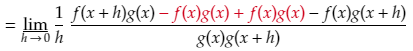
Now we swap the two denominators around – we are allowed to do this since we are multiplying fractions.

Next we use one of the properties of limits which says that the limit of a product of two functions is equal to the product of their limits. We then also use the fact that the limit as h approaches zero of g(x+h) is simply g(x)

Now we split the large fraction up, and take out a common g(x) from the first part and a common -f(x) from the second part.
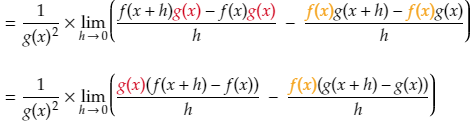
Another property of limits is that the limit of a sum is equal to the sum of the limits. So we can take the limit of each fraction separately.

And then we can take the limit of each part of the products
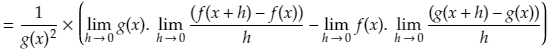
Now you may notice that two of the above limits look familiar – they are the exact definitions for f'(x) and g'(x).
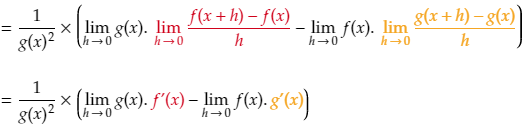
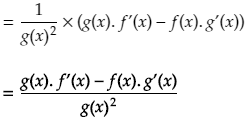
Proving the quotient rule using implicit differentiation and the product rule
Let y = f(x)/g(x), then we want to find y’.
First let’s rearrange the equation:
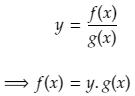
Now we can take the derivative on the left and right hand sides of the equation (by using the product rule on the right hand side)

Next, substitute y = f(x)/g(x) into the above equation
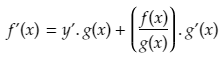
We ultimately want to find the derivative of y (y’) so now we solve for y’ and find the formula for the quotient rule.

Proving the quotient rule using the product and chain rules
Let F(x) = f(x)/g(x).
We can rewrite this quotient as a product

We can find F'(x) by using the product rule

To find (g(x)-1)’ we can apply the chain rule. The chain rule says we first take the derivative of g(x)-1 in terms of g(x) (= (-1)g(x)-2) and then multiply that by the derivative of g(x) in terms of x (= g'(x)).

Next we bring the negative exponents to the denominator and then simplify by finding the greatest common denominator. We are left with the formula for the quotient rule.
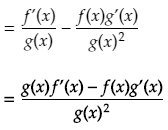
Proving the quotient rule using ln and the chain rule
Let y = f(x)/g(x)
To start, take the natural logarithm (ln) on both sides

Next apply the properties of logs to split the right hand side’s quotient to a difference of logs
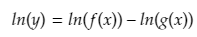
Now take the derivative on both sides. Recall that the derivative of ln(x) with respect to x is 1/x. In a similar way, the derivative of ln(y) with respect to y is 1/y, the derivative of ln(f(x)) with respect to f(x) is 1/f(x) and the derivative of ln(g(x)) with respect to g(x) is 1/g(x).
To find the derivatives of each of the terms with respect to x, we can apply the chain rule by first differentiating with respect to the inner function of ln, and then multiplying that by the derivative of the inner function.
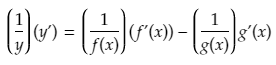
Lastly, isolate y’, substitute y = f(x)/g(x) in, and then simplify to solve for y’
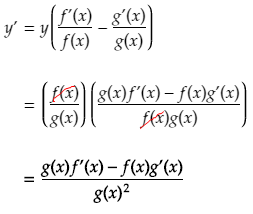
The quotient rule in terms of u and v
With regards to notation, the quotient rule is sometimes easier to express if you use u and v to represent the numerator and denominator respectively. This can be more compact than using the function notation f(x) and g(x).
Using the variable u for the numerator, and v for the denominator, the quotient rule for finding the derivative of the function u/v can be expressed as: