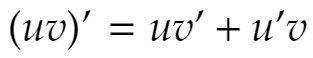The Product Rule

The product rule for calculus is useful for finding the derivative of a function which is expressed as the product of two differentiable functions.

Say for example we had two functions

f(x) = x and
g(x) = x²

Now say we wanted to find the derivative of

One approach to finding the derivative would be to simplify the function by multiplying it, and then differentiate the answer. Like this:

So the derivative of the product f(x).g(x) is 3x² (since the derivative of x³ is 3x².

Next, let’s calculate the derivative of f'(x).g'(x). In other words let’s differentiate each function first, and then multiply the derivatives together.

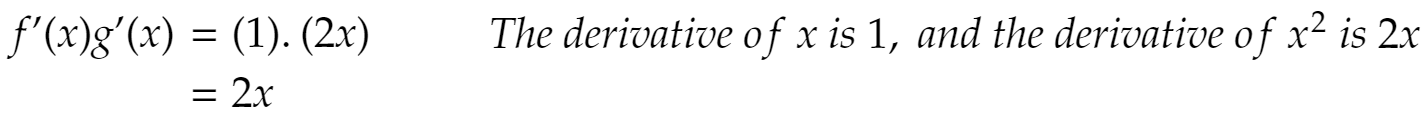
From the above we can see that (f(x)g(x))’ = 3x², and that is not equal to f'(x)g'(x) = 2x

The derivative of a product is not equal to the product of the derivatives

To differentiate a product, you cannot just take the derivative of the first function and multiply it by the derivative of the second function. Instead, we need to use the product rule to find the derivative of a product (in a similar way that the quotient rule needs to be used to find the derivative of a quotient).

The Product Rule Formula For Differentiation

If two functions f(x) and g(x) are differentiable (i.e. the derivatives of f(x) and g(x) exist), then their product f(x).g(x) is differentiable, and the derivative can be found as follows:

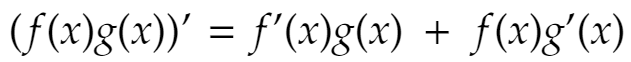
The formula for the product rule in words

The Product Rule states that the derivative of a product is equal to the derivative of the first function times the second function plus the first function times the derivative of the second function.

When To Use The Product Rule

In calculus, the product rule can be used when the function you want to differentiate consists of a product, and both parts of the product are differentiable functions of their own.

For example the function f(x) = x.x² can be differentiated using the product rule for derivatives because:

• The first function (x) is differentiable – its derivative is 1
• The second function (x²) is differentiable – it’s derivative is 2x

(Of course you could also first simplify the function to x³ and then differentiate it and get the same result)

Examples Using The Product Rule

The best way to understand how the product rule works is by looking at some examples.

Using the product rule

For the first example, let’s use the product rule to find the derivative of

The above function is actually a product of two other functions, namely x and cos(x)

We can call these two functions f(x) and g(x):
f(x) = x
g(x) = cos(x)

And the derivatives of these two functions are:
f'(x) = 1 (since the derivative of x is 1)
g'(x) = -sin(x) (since the derivative of cos(x) is -sin(x)

We can now apply the product rule to find the derivative of the function xcos(x) which is a product of f(x) and g(x).

The formula for the product rule is:

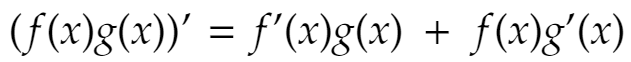
Next we plug f(x), f'(x), g(x) and g'(x) into the above formula:

And then we can simplify the above to get a final answer of:

Proof Of The Product Rule

Proving the product rule using first principles

Let F(x) = f(x)g(x)

The definition of the derivative of F(x) is

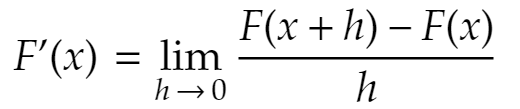
If we insert F(x) = f(x)g(x) into the definition we get:

This does not help us much in terms of simplification, so we need to pull a little trick to take this further.

What we do is we add 0 to the numerator, which of course does not change the value at all. The trick is to add 0 in the form of f(x+h)g(x) – f(x+h)g(x) instead of adding a straight 0. Note we also swap the order around (-f(x+h)g(x) + f(x+h)g(x)) to make things easier.

Next we use one of the properties of limits which states that the limit of a sum is equal to the sum of the limits. So we can split the above limit into two parts. Like this:

Now we can perform factorisation by taking out the term f(x+h) in the first numerator and g(x) in the second numerator.

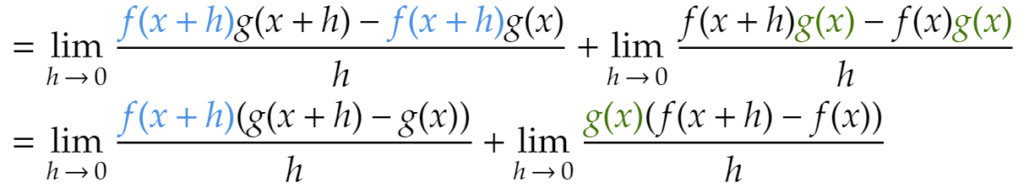
We now again apply a property of limits which says that the limit of a product of two functions is equal to the product of their limits. So each of the two terms above can be written as the products of two limits.

Now if we examine each of these limits individually:

Plugging these individual solutions to each of the limits from above gives us the final version of the product rule.

The Product Rule in Terms of u and v

With regards to notation, the product rule is sometimes easier to express if you use u and v to represent the two functions which make up the product. This can also be more compact than using the function notation f(x) and g(x).

Using the variable u for the first function of the product, and v for the second function of the product, the product rule for finding the derivative of the function uv can be expressed as: