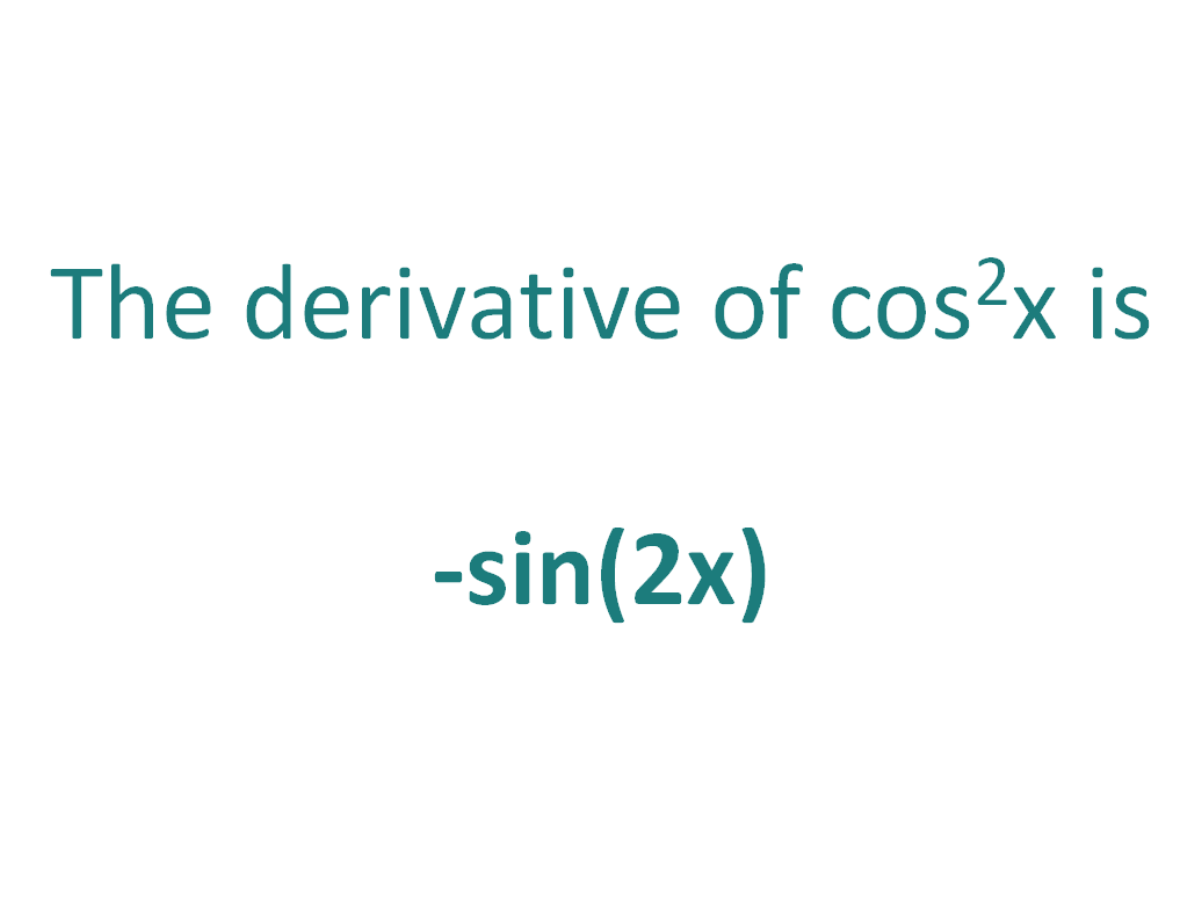The derivative of cos^2x is -sin(2x)
How to calculate the derivative of cos^2x
Note that in this post we will be looking at differentiating cos2(x) which is not the same as differentiating cos(2x). Here is our post dealing with how to differentiate cos(2x).
There are two methods that can be used for calculating the derivative of cos^2x.
The first method is by using the product rule for derivatives (since cos2(x) can be written as cos(x).cos(x)).
The second method is by using the chain rule for differentiation.
Finding the derivative of cos^2x using the product rule
The product rule for differentiation states that the derivative of f(x).g(x) is f’(x)g(x) + f(x).g’(x)
The Product Rule:
For two differentiable functions f(x) and g(x)
If F(x) = f(x).g(x)
Then the derivative of F(x) is F'(x) = f’(x)g(x) + f(x)g'(x)
First, let F(x) = cos2(x)
Then remember that cos2(x) is equal to cos(x).cos(x)
So F(x) = cos(x)cos(x)
By setting f(x) and g(x) as cos(x) means that F(x) = f(x).g(x) and we can apply the product rule to find F'(x)
| F'(x) | = f'(x)g(x) + f(x)g'(x) | Product Rule Definition |
| = f'(x)cos(x) + cos(x)g'(x) | f(x) = g(x) = cos(x) | |
| = -sin(x)cos(x) + cos(x)(-sin(x)) | f'(x) = g(‘x) = -sin(x) | |
| = -2sin(x)cos(x) | ||
| = –sin(2x) | Double angle identity: sin(2x) = 2sin(x)cos(x) |
Using the product rule, the derivative of cos^2x is -sin(2x)
Finding the derivative of cos^2x using the chain rule
The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.
In this case:
- We know how to differentiate cos(x) (the answer is -sin(x))
- We know how to differentiate x2 (the answer is 2x)
This means the chain rule will allow us to perform the differentiation of the expression cos^2x.
Using the chain rule to find the derivative of cos^2x
Although the expression cos2x contains no parenthesis, we can still view it as a composite function (a function of a function).
We can write cos2x as (cos(x))2.
Now the function is in the form of x2, except it does not have x as the base, instead it has another function of x (cos(x)) as the base.
Let’s call the function of the base g(x), which means:
g(x) = cos(x)
From this it follows that:
cos(x)2 = g(x)2
So if the function f(x) = x2 and the function g(x) = cos(x), then the function (cos(x))2 can be written as a composite function.
f(x) = x2
f(g(x)) = g(x)2 (but g(x) = cos(x))
f(g(x)) = (cos(x))2
Let’s define this composite function as F(x):
F(x) = f(g(x)) = (cos(x))2
We can find the derivative of cos^2x (F'(x)) by making use of the chain rule.
The Chain Rule:
For two differentiable functions f(x) and g(x)
If F(x) = f(g(x))
Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)
Now we can just plug f(x) and g(x) into the chain rule.
How to find the derivative of cos^2x using the Chain Rule:
| F'(x) | = f'(g(x)).g'(x) | Chain Rule Definition |
| = f'(g(x))(-sin(x)) | g(x) = cos(x) ⇒ g'(x) = sin(x) | |
| = (2cos(x)).(-sin(x)) | f(g(x)) = (cos(x))2 ⇒ f'(g(x)) = 2cos(x) | |
| = -2cos(x)sin(x) | ||
| = -sin(2x) | Double angle identity: sin(2x) = 2sin(x)cos(x) |
Using the chain rule, the derivative of cos^2x is -sin(2x)
Finally, just a note on syntax and notation: cos^2x is sometimes written in the forms below (with the derivative as per the calculations above). Just be aware that not all of the forms below are mathematically correct.
| cos2x | ► Derivative of cos2x = -sin(2x) |
| cos^2(x) | ► Derivative of cos^2(x) = -sin(2x) |
| cos 2 x | ► Derivative of cos 2 x = -sin(2x) |
| (cosx)^2 | ► Derivative of (cosx)^2 = -sin(2x) |
| cos squared x | ► Derivative of cos squared x = -sin(2x) |
| cosx2 | ► Derivative of cosx2 = -sin(2x) |
| cos^2 | ► Derivative of cos^2 = -sin(2x) |
The Second Derivative Of cos^2x
To calculate the second derivative of a function, you just differentiate the first derivative.
From above, we found that the first derivative of cos^2x = -sin(2x). So to find the second derivative of cos^2x, we just need to differentiate -sin(2x)
We can use the chain rule to find the derivative of -sin(2x).
We can set g(x) = 2x and f(x) = -sin(x). the F(x) = f(g(x)) = -sin(2x). We can then apply the chain rule to find F'(x).
The chain rules says that the derivative of F(x) is equal to f’(g(x)).g'(x).
f'(g(x)).g'(x)
= -cos(2x).2
= -2cos(2x)
► The second derivative of cos^2x is -2cos(2x)