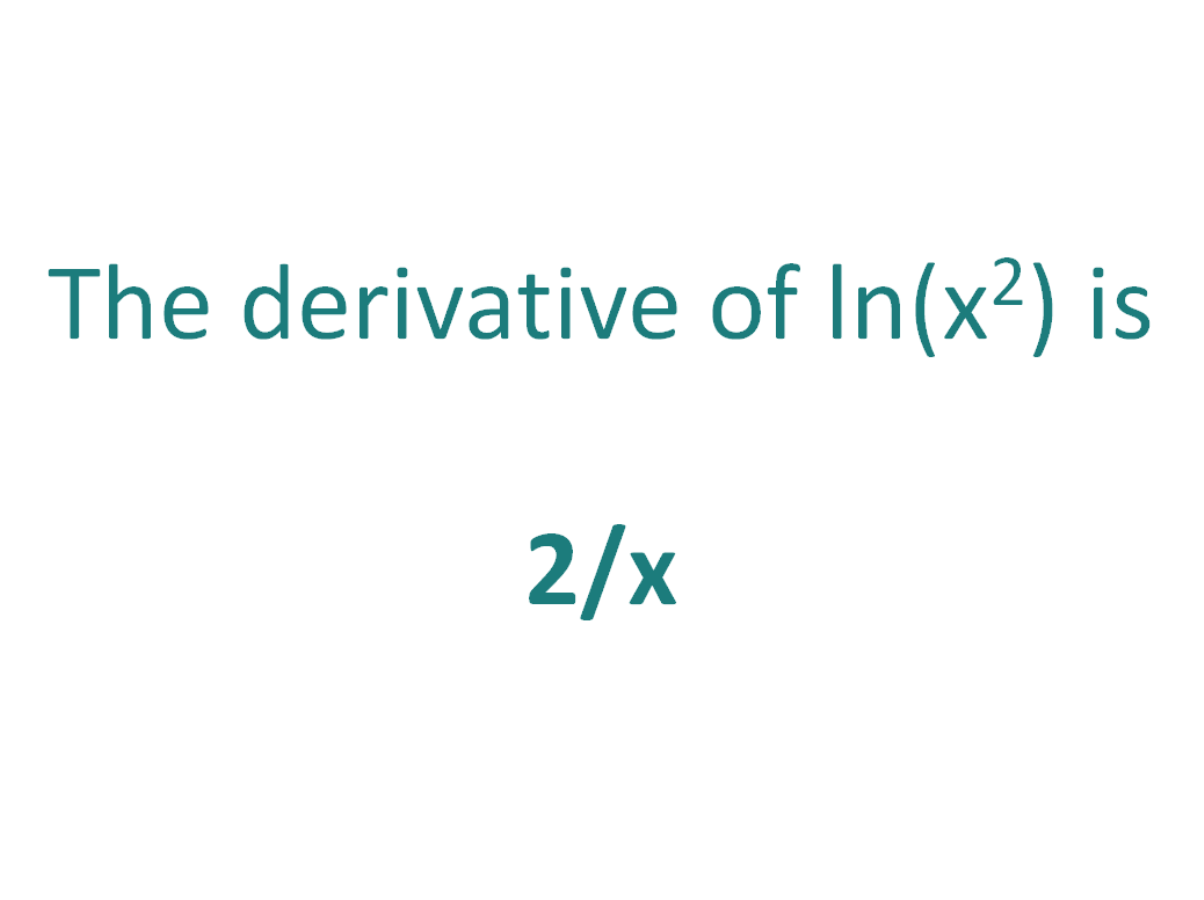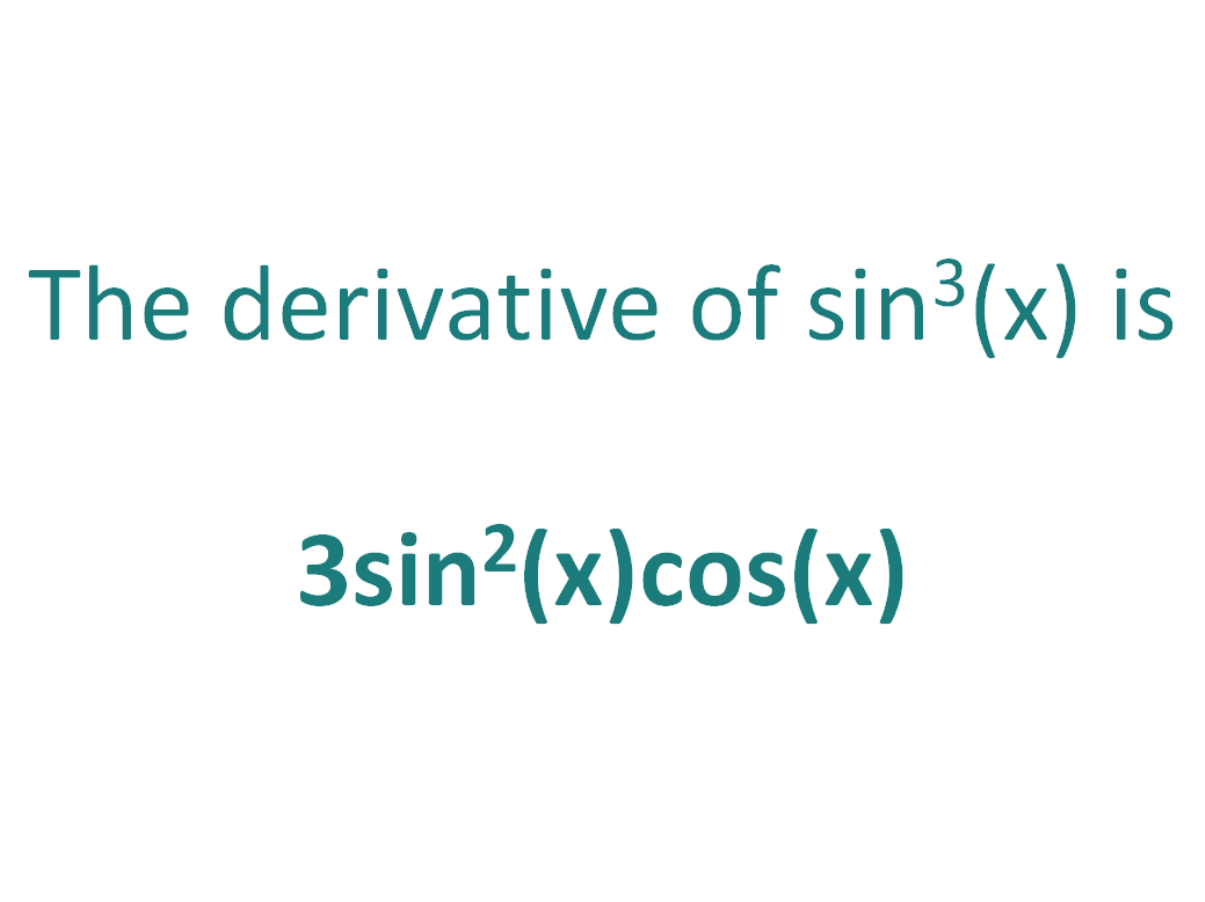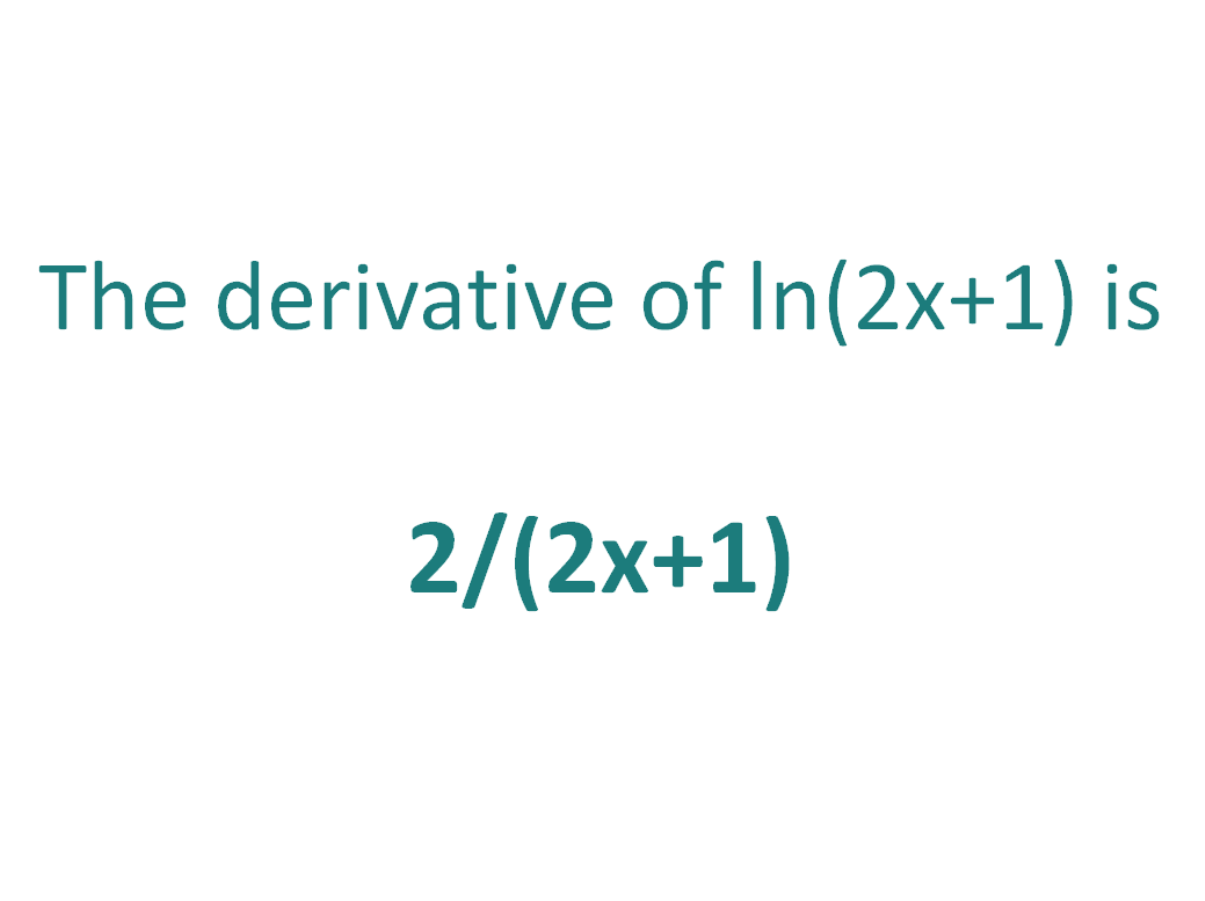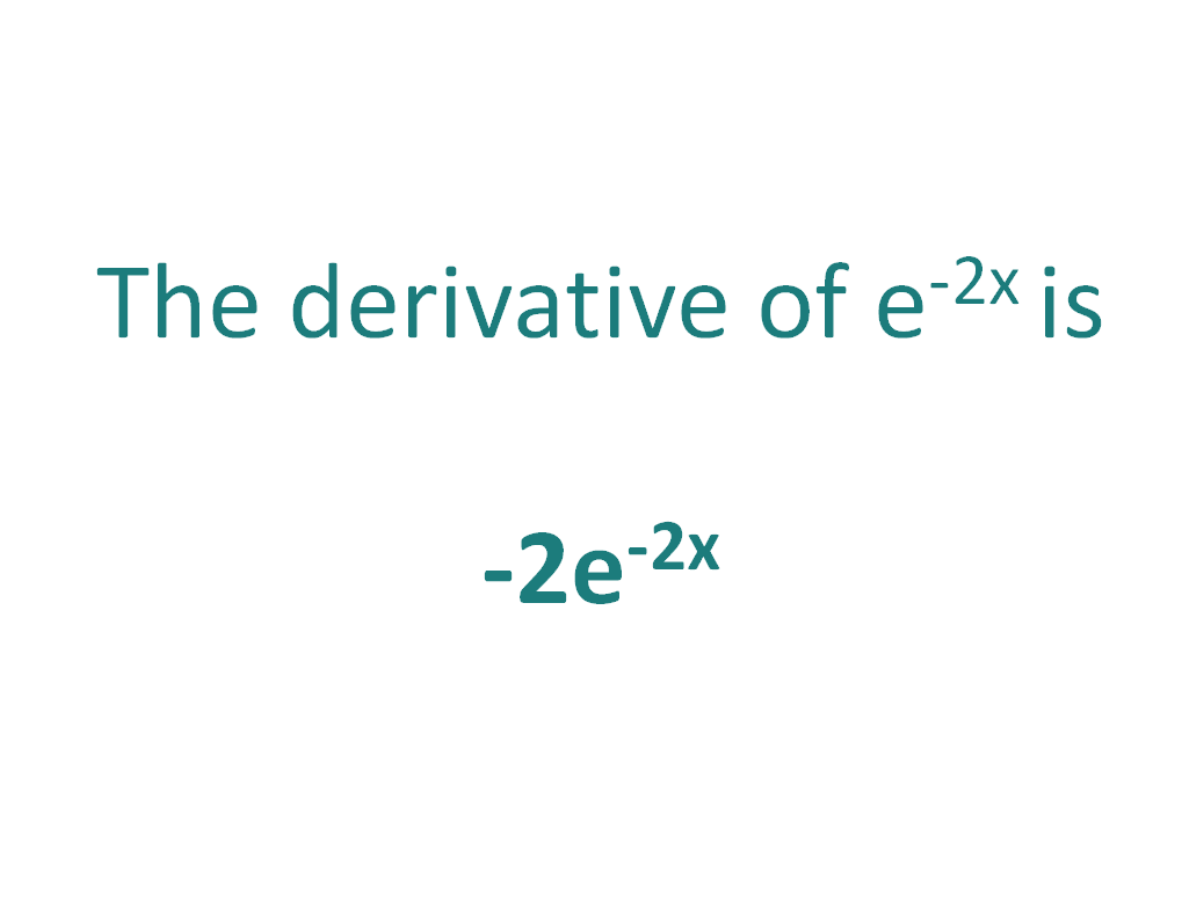The derivative of ln(x^2) is 2/x
How to calculate the derivative of lnx^2
Note that in this post we will be looking at differentiating ln(x2) which is not the same as differentiating ln2(x) or ln(2x). Here are our posts dealing with how to differentiate ln2(x) and how to differentiate ln(2x)
There are two methods that can be used for calculating the derivative of ln(x2).
The first method is by using the chain rule for derivatives.
The second method is by using the properties of logs to write ln(x2) into a form which differentiable without needing to use the chain rule.
Finding the derivative of ln(x2) using the chain rule
The chain rule is useful for finding the derivative of an expression which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.
In this case:
- We know how to differentiate x2(the answer is 2x)
- We know how to differentiate ln(x) (the answer is 1/x)
This means the chain rule will allow us to perform the differentiation of the function ln(x2).
To perform the differentiation, the chain rule says we must differentiate the expression as if it were just in terms of x as long as we then multiply that result by the derivative of what the expression was actually in terms of (in this case the derivative of x2).
Using the chain rule to find the derivative of ln(x^2)
ln(x2) is in the form of the standard natural log function ln(x), except it does not have x as an argument, instead it has another function of x (x2).
Let’s call the function in the argument g(x), which means:
g(x) = x2
From this it follows that:
ln(x2) = ln(g(x))
So if the function f(x) = ln(x) and the function g(x) = x2, then the function ln(x2) can be written as a composite function.
f(x) = ln(x)
f(g(x)) = ln(g(x)) (but g(x) = x2)
f(g(x)) = ln(x2)
Let’s define this composite function as F(x):
F(x) = f(g(x)) = ln(x2)
We can find the derivative of ln(x2) (F'(x)) by making use of the chain rule.
The Chain Rule:
For two differentiable functions f(x) and g(x)
If F(x) = f(g(x))
Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)
Now we can just plug f(x) and g(x) into the chain rule. But before we do that, just a recap on the derivative of the natural logarithm.
The derivative of ln(x) with respect to x is (1/x)
The derivative of ln(s) with respect to s is (1/s)
In a similar way, the derivative of ln(x2) with respect to x2 is (1/x2).
We will use this fact as part of the chain rule to find the derivative of ln(x2) with respect to x.
How to find the derivative of ln(x2) using the Chain Rule:
| F'(x) | = f'(g(x)).g'(x) | Chain Rule Definition |
| = f'(g(x)).(2x) | g(x) = x2⇒ g'(x) = 2x | |
| = (1/x2).2x | f(g(x)) = ln(x2) ⇒ f'(g(x)) = 1/x2 (The derivative of ln(x2) with respect to x2is (1/x2)) | |
| = 2/x |
Using the chain rule, we find that the derivative of ln(x2) is 2/x
Finally, just a note on syntax and notation: ln(x^2) is sometimes written in the forms below (with the derivative as per the calculations above). Just be aware that not all of the forms below are mathematically correct.
| ln(x2) | ► Derivative of ln(x2) = 2/x |
| lnx2 | ► Derivative of lnx2 = 2/x |
| lnx^2 | ► Derivative of lnx^2 = 2/x |
| ln x 2 | ► Derivative of ln x 2 = 2/x |
| ln x squared | ► Derivative of ln x squared = 2/x |
Finding the derivative of ln(x2) using log properties
Since ln is the natural logarithm, the usual properties of logs apply.
The power property of logs states that ln(xy) = y.ln(x). In other words taking the log of x to a power is the same as multiplying the log of x by that power.
We can therefore use the power rule of logs to rewrite ln(x2) as:
f(x) = ln(x2) = 2.ln(x)
How to find the derivative of ln(x2) using the power rule of logs
| f(x) | = 2ln(x) | |
| f'(x) | = 2.(1/x) | The derivative of ln(x) is 1/x |
| = 2/x |
The Second Derivative of ln(x2)
To calculate the second derivative of a function, you just differentiate the first derivative.
From above, we found that the first derivative of ln(x2) = 2/x. So to find the second derivative of ln(x2), we just need to differentiate 2/x
If we differentiate 2/x we get an answer of (-2/x2).
► The second derivative of ln(x2) = -2/x2