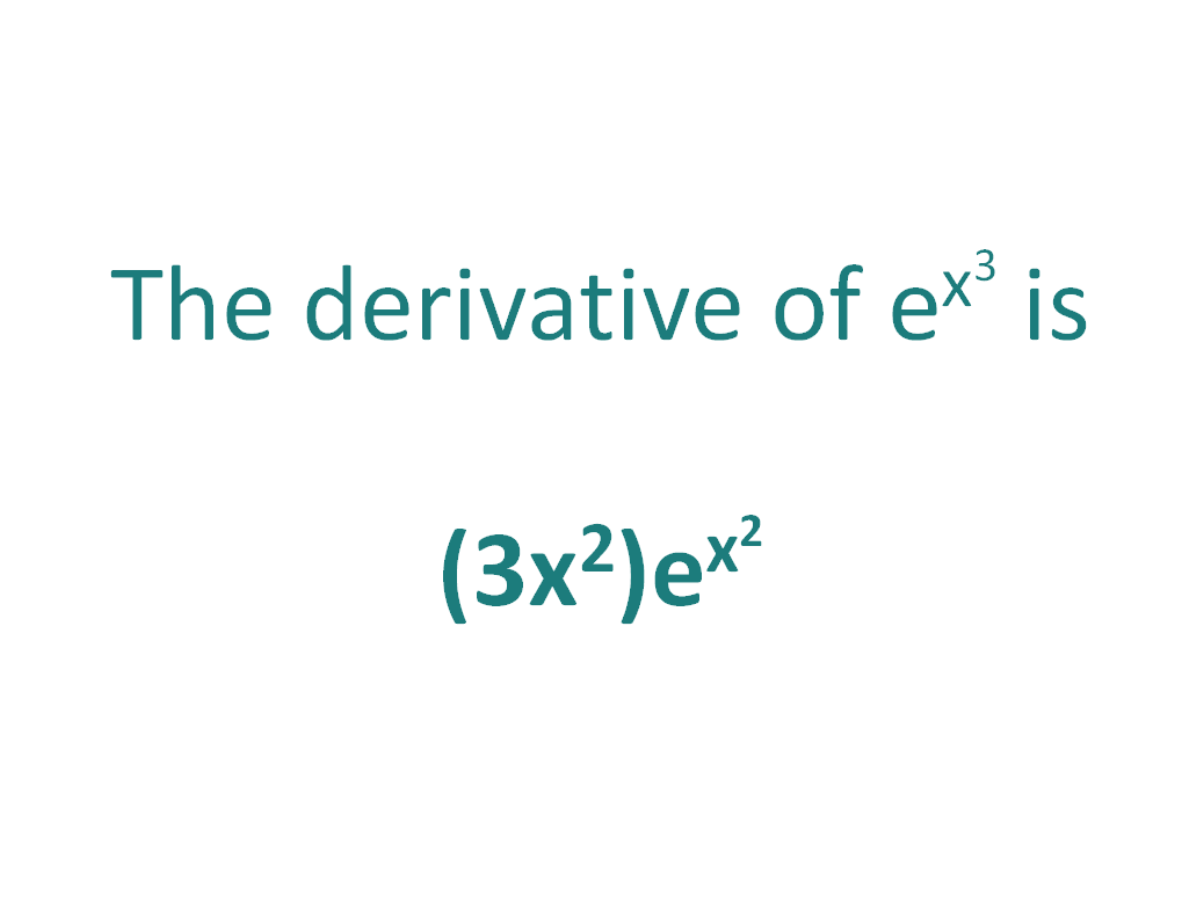The derivative of e^x^3 is (3x^2)(e^x^3)
How to calculate the derivative of e^x^3
The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.
In this case:
- We know how to differentiate ex (the answer is ex)
- We know how to differentiate x3 (the answer is 3x)
Because e^x^3 is a function which is a combination of ex and x3, it means we can perform the differentiation of e to the x3 by making use of the chain rule.
Using the chain rule to find the derivative of e^x^3
Although the function ex3 contains no parenthesis, we can still view it as a composite function (a function of a function).
If we add parenthesis around the exponent, we get e(x3).
Now the function is in the form of the standard exponential function ex, except it does not have x as an exponent, instead the exponent is another function of x (x3).
Let’s call the function in the exponent g(x), which means:
g(x) = x3
From this it follows that:
ex3 = eg(x)
Let’s set f(x) = ex.
Then, because g(x) = x3, the function ex3 can be written as a composite function of f(x) and g(x).
f(x) = ex
f(g(x)) = eg(x) (but g(x) = x3)
Therefore, f(g(x)) = ex3
Let’s define this composite function as F(x):
F(x) = f(g(x)) = ex3
We can now find the derivative of F(x) = e^x^3, F'(x), by making use of the chain rule.
The Chain Rule:
For two differentiable functions f(x) and g(x)
If F(x) = f(g(x))
Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)
Now we can just plug f(x) and g(x) into the chain rule to find the derivative of e to the x squared.
How to find the derivative of e^x^3 using the Chain Rule:
| F'(x) | = f'(g(x)).g'(x) | Chain Rule Definition |
| = f'(g(x))(3x2) | g(x) = x3 ⇒ g'(x) = 3x2 | |
| = (e^x^3).(3x2) | f(g(x)) = e^x^3 ⇒ f'(g(x)) = e^x^3 | |
| = (3x2)ex3 |
Using the chain rule, the derivative of e^x^3 is (3x2)ex3
Finally, just a note on syntax and notation: the exponential function e^x^3 is sometimes written in the forms shown below (the derivative of each is as per the calculations above). Just be aware that not all of the forms below are mathematically correct.
| ex3 | ► Derivative of ex3 =(3x2)ex3 |
| e^(x^3) | ► Derivative of e^(x^3) = (3x2)ex3 |
| e x 3 | ► Derivative of e x 3 = (3x2)ex3 |
| e to the x cubed | ► Derivative of e to the x cubed = (3x2)ex3 |
The Second Derivative of e^x^3
To calculate the second derivative of a function, you just differentiate the first derivative.
From above, we found that the first derivative of e^x^3 = (3x2)ex3. So to find the second derivative of e^x^3, we just need to differentiate (3x2)ex3.
We can use the chain rule in combination with the product rule for differentiation to calculate the derivative of (3x2)ex3. The answer is (6x)ex3 + (9x4)ex3
► The second derivative of e^x^3 = (6x)ex3 + (9x4)ex3