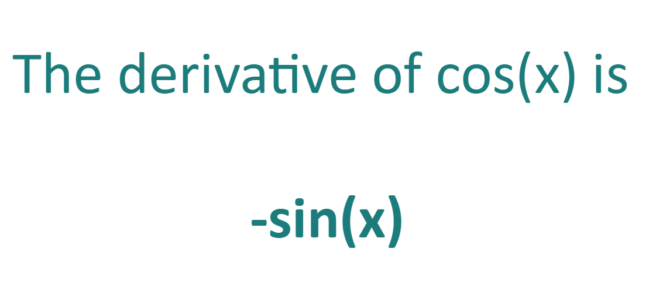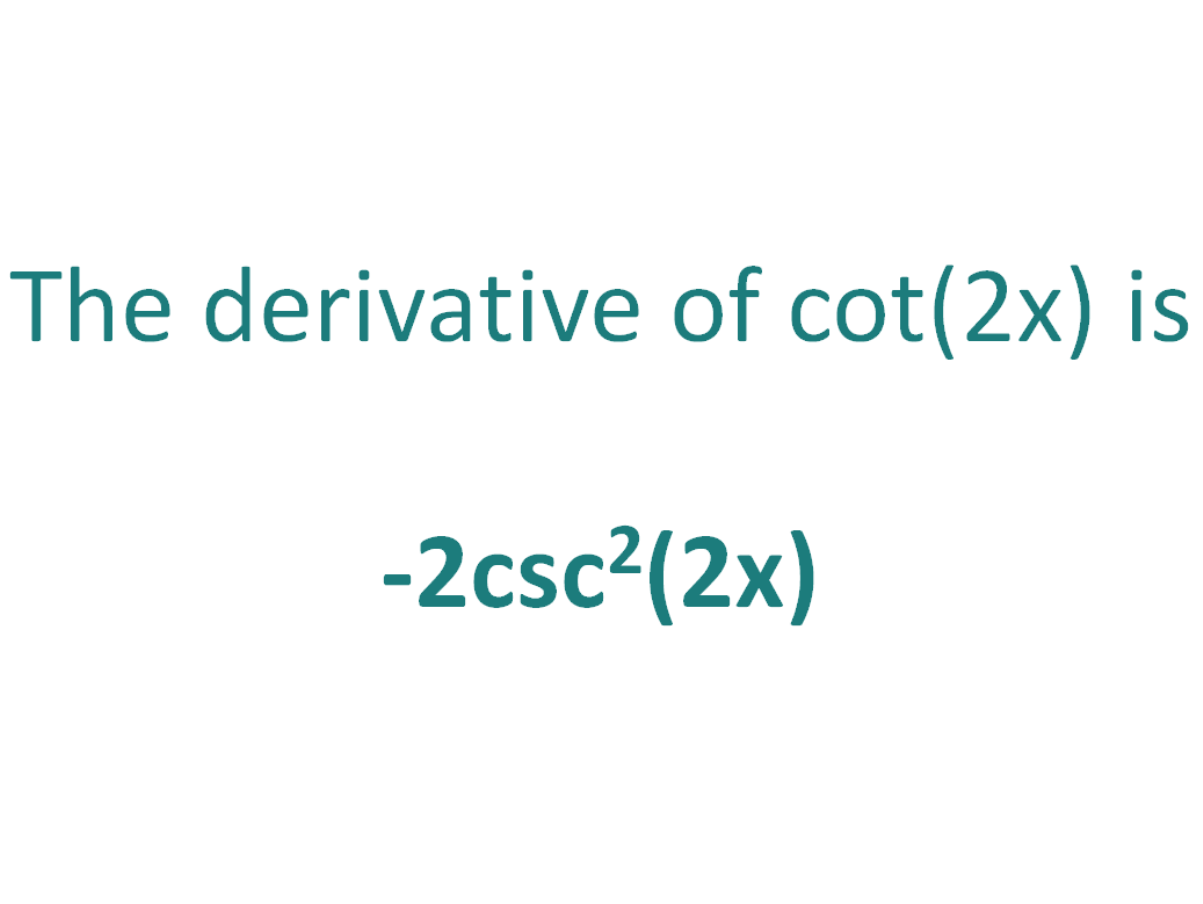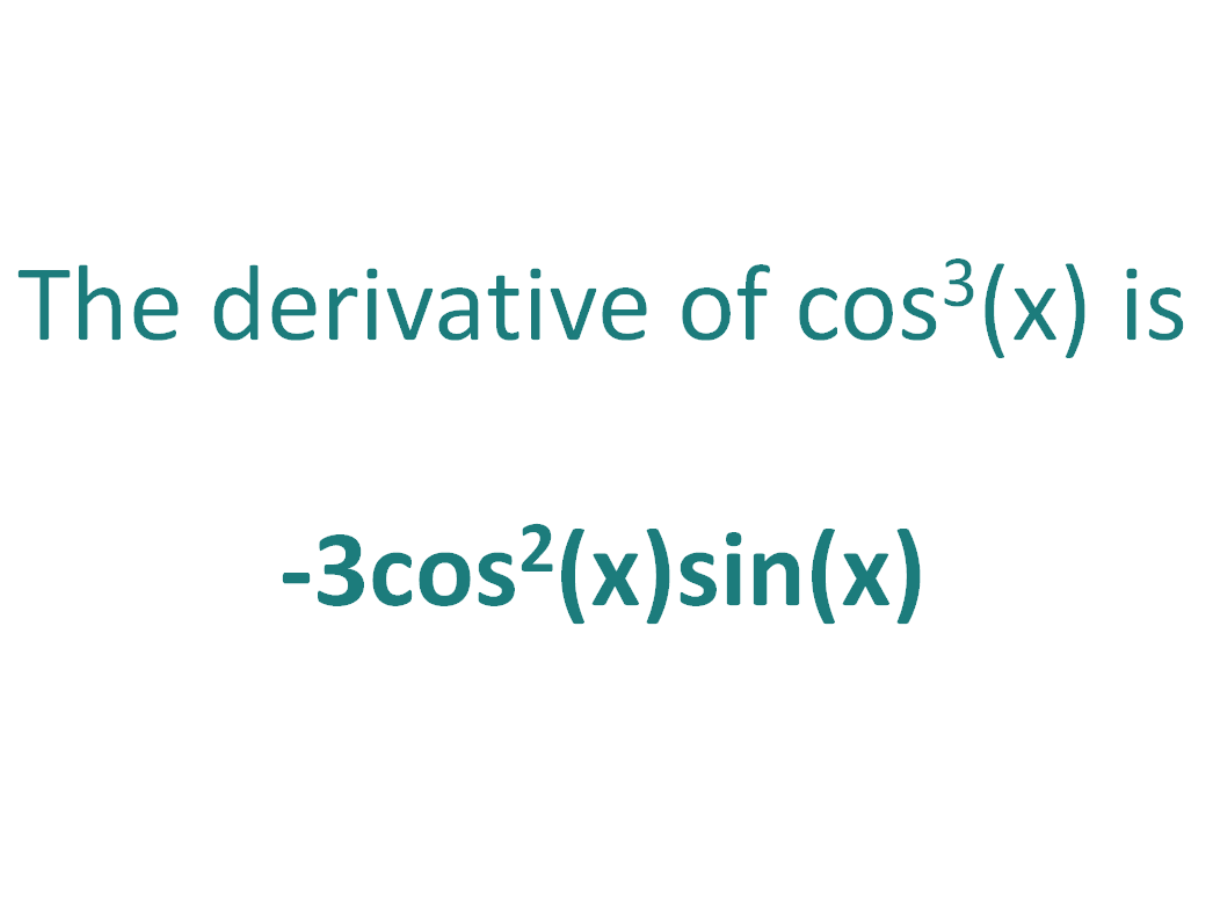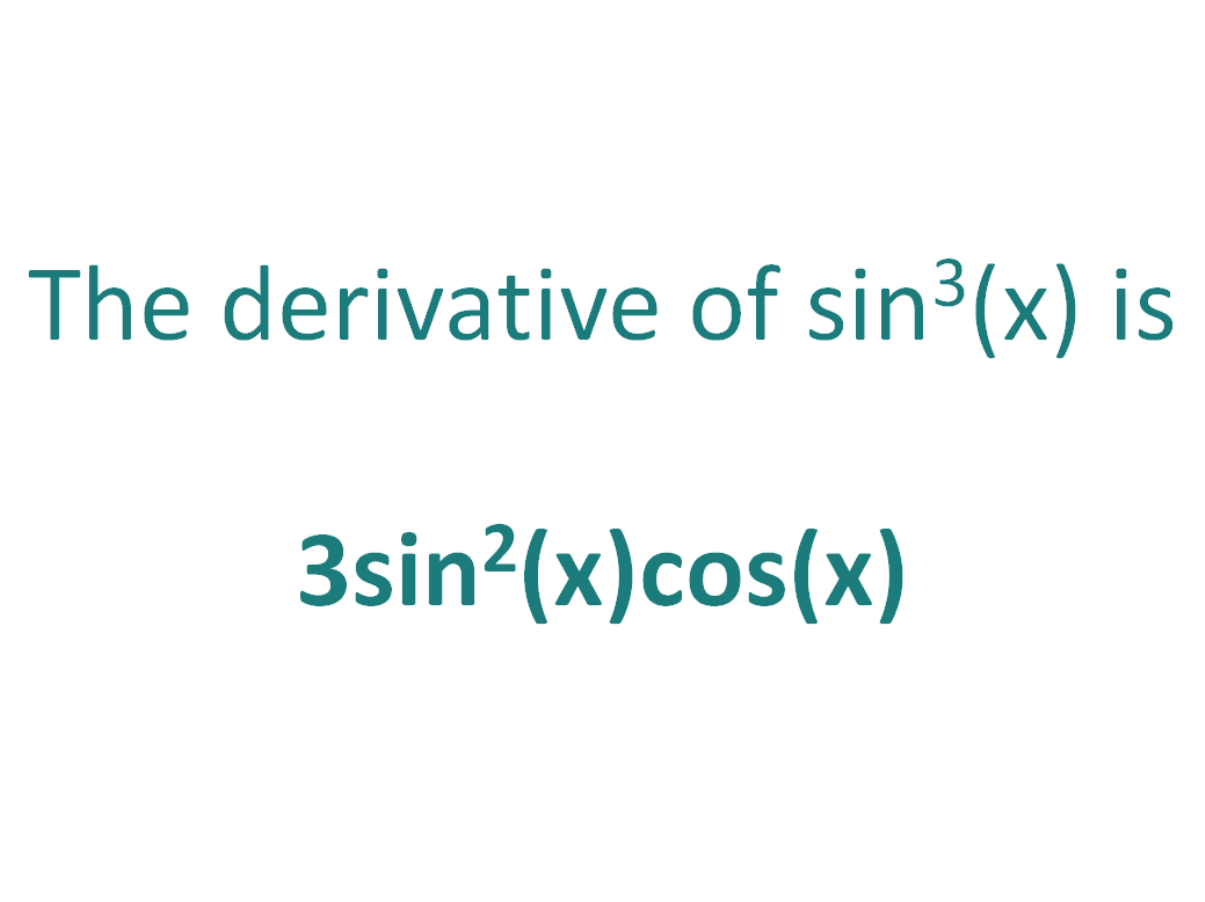What is the derivative of Cos?

In calculus, the derivative of cos(x) is equal to -sin(x)

(d/dx)cos(x) = -sin(x)

Or

cos'(x) = -sin(x)

So what does this mean and how do we get to that answer?

Well, since differentiation involves finding the rate of change (or gradient) of a function, finding the derivative of cos means that we are trying to determine the rate of change of the cos function with respect to x (the angle of the cos function).

This evaluation of the rate of change of the cos function with respect to the variable x is found to be negative sine of x (-sin(x)).

Next we will look at how we calculate the derivative of cos(x).

The derivative of cos(x) from first principles

To find the derivative of cos(x) (or in fact any function) it is often a good idea to start with first principles and the definition of the derivative of a function.

Recall that derivative of a function f(x) (or f'(x)) can be expressed as

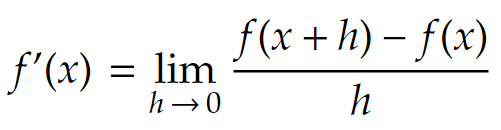
In this case f(x), the function we want to differentiate is cos(x). So if we put f(x) = cos(x) into the definition of the derivative function we get

Next, we need to use the following trigonomic identity relating to cos and the sum of two angles. You may recall (if you don’t then just accept it as fact for now)

We can then apply this trig identity to the cos(x+h) term from above to get:

Then we can do some factorisation of the numerator by rearranging it a little and taking out a common cos(x) term:

Finally, we split the numerator up so that we can apply two formulas related to finding the limits of trigonometric functions.

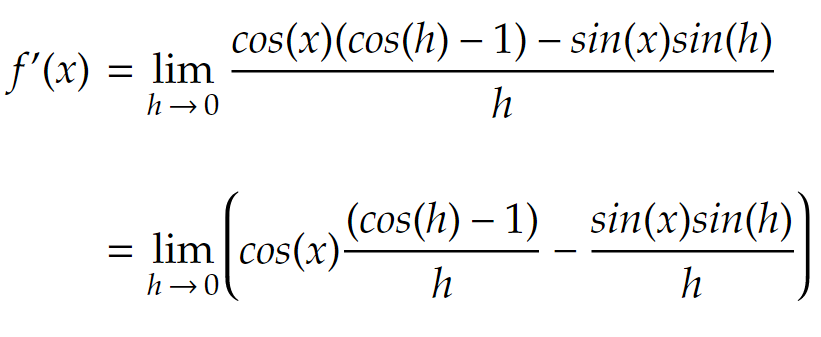
The following two formulas relating to limits of sin and cos now come in handy. We can plug these two in and then solve:

And that proves that the derivative of cos(x) is -sin(x)

---

The derivative of csc(3x) is -3cot(3x)csc(3x)

---

How to calculate the derivative of csc(3x)

The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.

In this case:

• We know how to differentiate csc(x) (the answer is -csc(x)cot(x))
• We know how to differentiate 3x (the answer is 3)

This means the chain rule will allow us to perform the differentiation of the expression csc(3x).

Using the chain rule to find the derivative of csc(3x)

To perform the differentiation csc(3x), the chain rule says we must differentiate the expression as if it were just in terms of x as long as we then multiply that result by the derivative of what the expression is actually in terms of (in this case the derivative of 3x).

Let’s call the function in the argument of csc, g(x), which means the function is in the form of csc(x), except it does not have x as the angle, instead it has another function of x (3x) as the angle

If:

g(x) = 3x

It follows that:

csc(3x) = csc(g(x))

So if the function f(x) = cosec(x) and the function g(x) = 3x, then the function csc(3x) can be written as a composite function.

f(x) = csc(x)

f(g(x)) = csc(g(x)) (but g(x) = 3x)

f(g(x)) = csc(3x)

Let’s define this composite function as F(x):

F(x) = f(g(x)) = csc(3x)

We can find the derivative of csc(3x) (F'(x)) by making use of the chain rule.

---

The Chain Rule:
For two differentiable functions f(x) and g(x)

If F(x) = f(g(x))

Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)

---

Now we can just plug f(x) and g(x) into the chain rule.

How to find the derivative of csc(3x) using the Chain Rule:

F'(x)	= f'(g(x)).g'(x)	Chain Rule Definition
	= f'(g(x))(3)	g(x) = 3x ⇒ g'(x) = 3
	= (-cot(3x)csc(3x)).(3)	f(g(x)) = csc(3x) ⇒ f'(g(x)) = -cot(3x)csc(3x)
	= -3cot(3x)csc(3x)

Using the chain rule, the derivative of csc(3x) is -3cot(3x)csc(3x)

---

Finally, just a note on syntax and notation: csc(3x) is sometimes written in the forms below (with the derivative as per the calculations above). Just be aware that not all of the forms below are mathematically correct.

csc3x	► Derivative of csc3x = -3cot(3x)csc(3x)
csc 3 x	► Derivative of csc 3 x = -3cot(3x)csc(3x)
csc 3x	► Derivative of csc 3x = -3cot(3x)csc(3x)
csc (3x)	► Derivative of csc (3x) = -3cot(3x)csc(3x)
cosec(3x)	► Derivative of cosec(3x) = -3cot(3x)csc(3x)

The Second Derivative Of csc(3x)

To calculate the second derivative of a function, differentiate the first derivative.

From above, we found that the first derivative of csc(3x) = -3cot(3x)csc(3x). So to find the second derivative of csc(3x), we need to differentiate -3cot(3x)csc(3x).

We can use the product and chain rules, and then simplify to find the derivative of -3cot(3x)csc(3x) is 9csc³(3x) + 9cot²(3x)csc(3x)

► The second derivative of csc(3x) is 9csc³(3x) + 9cot²(3x)csc(3x)

---

The derivative of tan(3x) is 3sec²(3x)

---

How to calculate the derivative of tan(3x)

The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.

In this case:

• We know how to differentiate tan(x) (the answer is sec²(x))
• We know how to differentiate 3x (the answer is 3)

This means the chain rule will allow us to differentiate the expression tan(3x).

Using the chain rule to find the derivative of tan(3x)

To perform the differentiation tan(3x), the chain rule says we must differentiate the expression as if it were just in terms of x as long as we then multiply that result by the derivative of what the expression is actually in terms of (in this case the derivative of 3x).

Let’s call the function in the argument of tan, g(x), which means the function is in the form of tan(x), except it does not have x as the angle, instead it has another function of x (3x) as the angle

If:

g(x) = 3x

It follows that:

tan(3x) = tan(g(x))

So if the function f(x) = tan(x) and the function g(x) = 3x, then the function tan(3x) can be written as a composite function.

f(x) = tan(x)

f(g(x)) = tan(g(x)) (but g(x) = 3x))

f(g(x)) = tan(3x)

Let’s define this composite function as F(x):

F(x) = f(g(x)) = tan(3x)

We can find the derivative of tan(3x) (F'(x)) by making use of the chain rule.

---

The Chain Rule:
For two differentiable functions f(x) and g(x)

If F(x) = f(g(x))

Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)

---

Now we can just plug f(x) and g(x) into the chain rule. But before we do that, just a quick recap on the derivative of the tan function.

The derivative of tan(x) with respect to x is sec²(x)
The derivative of tan(z) with respect to z is sec²(z)

In a similar way, the derivative of tan(3x) with respect to 3x is sec²(3x).

We will use this fact as part of the chain rule to find the derivative of tan(3x) with respect to x.

How to find the derivative of tan(3x) using the Chain Rule:

F'(x)	= f'(g(x)).g'(x)	Chain Rule Definition
	= f'(g(x))(3)	g(x) = 3x ⇒ g'(x) = 3
	= (sec2(3x)).(3)	f(g(x)) = tan(3x) ⇒ f'(g(x)) = sec2(3x)
	= 3sec2(3x)

Using the chain rule, the derivative of tan(3x) is 3sec²(3x)

---

Finally, just a note on syntax and notation: tan(3x) is sometimes written in the forms below (with the derivative as per the calculation above). Just be aware that not all of the forms below are mathematically correct.

tan3x	► Derivative of tan3x = 3sec2(3x)
tan 3 x	► Derivative of tan 3 x = 3sec2(3x)
tan 3x	► Derivative of tan 3x = 3sec2(3x)
tan (3x)	► Derivative of tan (3x) = 3sec2(3x)

The Second Derivative Of tan(3x)

To calculate the second derivative of a function, you just differentiate the first derivative.

From above, we found that the first derivative of tan(3x) = 3sec²(3x). So to find the second derivative of tan(3x), we just need to differentiate 3sec²(3x).

We can use the chain rule to find the derivative of 3sec²(3x) (bearing in mind that the derivative of sec^2(x) is 2sec²(x)tan(x)) and it gives us a result of 18sec²(3x)tan(3x)

► The second derivative of tan(2x) is 18sec²(3x)tan(3x)

---

The derivative of cot(2x) is -2csc²(2x)

---

How to calculate the derivative of cot(2x)

Note that in this post we will be looking at differentiating cot(2x) which is not the same as differentiating cot²(x). Here is our post dealing with how to differentiate cot^2(x).

The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.

In this case:

• We know how to differentiate cot(x) (the answer is cosec²(x))
• We know how to differentiate 2x (the answer is 2)

This means the chain rule will allow us to differentiate the expression cot(2x).

Using the chain rule to find the derivative of cot(2x)

To perform the differentiation cot(2x), the chain rule says we must differentiate the expression as if it were just in terms of x as long as we then multiply that result by the derivative of what the expression is actually in terms of (in this case the derivative of 2x).

Let’s call the function in the argument of cot, g(x), which means the function is in the form of cot(x), except it does not have x as the angle, instead it has another function of x (2x) as the angle

If:

g(x) = 2x

It follows that:

cot(2x) = cot(g(x))

So if the function f(x) = cot(x) and the function g(x) = 2x, then the function cot(2x) can be written as a composite function.

f(x) = cot(x)

f(g(x)) = cot(g(x)) (but g(x) = 2x))

f(g(x)) = cot(2x)

Let’s define this composite function as F(x):

F(x) = f(g(x)) = cot(2x)

We can find the derivative of cot(2x) (F'(x)) by making use of the chain rule.

---

The Chain Rule:
For two differentiable functions f(x) and g(x)

If F(x) = f(g(x))

Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)

---

Now we can just plug f(x) and g(x) into the chain rule. But before we do that, just a quick recap on the derivative of the cot function.

The derivative of cot(x) with respect to x is -csc²(x)
The derivative of cot(z) with respect to z is -csc²(z)

In a similar way, the derivative of cot(2x) with respect to 2x is -csc²(2x).

We will use this fact as part of the chain rule to find the derivative of cot(2x) with respect to x.

How to find the derivative of cot(2x) using the Chain Rule:

F'(x)	= f'(g(x)).g'(x)	Chain Rule Definition
	= f'(g(x))(2)	g(x) = 2x ⇒ g'(x) = 2
	= (-csc2(2x)).(2)	f(g(x)) = cot(2x) ⇒ f'(g(x)) = -cosec2(2x)
	= -2csc2(2x)

Using the chain rule, the derivative of cot(2x) is -2csc²(2x)

---

Finally, just a note on syntax and notation: cot(2x) is sometimes written in the forms below (with the derivative as per the calculation above). Just be aware that not all of the forms below are mathematically correct.

cot2x	► Derivative of cot2x = -2csc2(2x)
cot 2 x	► Derivative of cot 2 x = -2csc2(2x)
cot 2x	► Derivative of cot 2x = -2csc2(2x)
cot (2x)	► Derivative of cot (2x) = -2csc2(2x)

The Second Derivative Of cot(2x)

To calculate the second derivative of a function, you just differentiate the first derivative.

From above, we found that the first derivative of cot(2x) = -2csc²(2x). So to find the second derivative of cot(2x), we just need to differentiate -2csc²(2x).

We can use the chain rule to find the derivative of -2csc(2x) (bearing in mind that the derivative of csc^2(x) is -2csc²(x)cot(x)) and it gives us a result of 8csc²(2x)cot(2x)

► The second derivative of cot(2x) is 8csc²(2x)cot(2x)

---

The derivative of csc(2x) is -2cot(2x)csc(2x)

---

How to calculate the derivative of csc(2x)

Note that in this post we will be looking at differentiating csc(2x) which is not the same as differentiating csc²(x). Here is our post dealing with how to differentiate csc^2(x).

The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.

In this case:

• We know how to differentiate csc(x) (the answer is -csc(x)cot(x))
• We know how to differentiate 2x (the answer is 2)

This means the chain rule will allow us to perform the differentiation of the expression csc(2x).

Using the chain rule to find the derivative of csc(2x)

To perform the differentiation csc(2x), the chain rule says we must differentiate the expression as if it were just in terms of x as long as we then multiply that result by the derivative of what the expression is actually in terms of (in this case the derivative of 2x).

Let’s call the function in the argument of csc, g(x), which means the function is in the form of csc(x), except it does not have x as the angle, instead it has another function of x (2x) as the angle

If:

g(x) = 2x

It follows that:

csc(2x) = csc(g(x))

So if the function f(x) = cosec(x) and the function g(x) = 2x, then the function csc(2x) can be written as a composite function.

f(x) = csc(x)

f(g(x)) = csc(g(x)) (but g(x) = 2x)

f(g(x)) = csc(2x)

Let’s define this composite function as F(x):

F(x) = f(g(x)) = csc(2x)

We can find the derivative of csc(2x) (F'(x)) by making use of the chain rule.

---

The Chain Rule:
For two differentiable functions f(x) and g(x)

If F(x) = f(g(x))

Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)

---

Now we can just plug f(x) and g(x) into the chain rule.

How to find the derivative of csc(2x) using the Chain Rule:

F'(x)	= f'(g(x)).g'(x)	Chain Rule Definition
	= f'(g(x))(2)	g(x) = 2x ⇒ g'(x) = 2
	= (-cot(2x)csc(2x)).(2)	f(g(x)) = csc(2x) ⇒ f'(g(x)) = -cot(2x)csc(2x)
	= -2cot(2x)csc(2x)

Using the chain rule, the derivative of csc(2x) is -2cot(2x)csc(2x)

---

Finally, just a note on syntax and notation: csc(2x) is sometimes written in the forms below (with the derivative as per the calculations above). Just be aware that not all of the forms below are mathematically correct.

csc2x	► Derivative of csc2x = -2cot(2x)csc(2x)
csc 2 x	► Derivative of csc 2 x = -2cot(2x)csc(2x)
csc 2x	► Derivative of csc 2x = -2cot(2x)csc(2x)
csc (2x)	► Derivative of csc (2x) = -2cot(2x)csc(2x)
cosec(2x)	► Derivative of cosec(2x) = -2cot(2x)csc(2x)

The Second Derivative Of csc(2x)

To calculate the second derivative of a function, differentiate the first derivative.

From above, we found that the first derivative of csc(2x) = -2cot(2x)csc(2x). So to find the second derivative of csc(2x), we need to differentiate -2cot(2x)csc(2x).

We can use the product and chain rules, and then simplify to find the derivative of -2cot(2x)csc(2x) is 4csc³(2x) + 4cot²(2x)csc(2x)

► The second derivative of csc(2x) is 4csc³(2x) + 4cot²(2x)csc(2x)

---

The derivative of sec(2x) is 2sec(2x)tan(2x)

---

How to calculate the derivative of sec(2x)

Note that in this post we will be looking at differentiating sec(2x) which is not the same as differentiating sec²(x). Here is our post dealing with how to differentiate sec^2(x).

The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.

In this case:

• We know how to differentiate sec(x) (the answer is sec(x)tan(x))
• We know how to differentiate 2x (the answer is 2)

This means the chain rule will allow us to differentiate the expression sec(2x).

Using the chain rule to find the derivative of sec(2x)

To perform the differentiation sec(2x), the chain rule says we must differentiate the expression as if it were just in terms of x as long as we then multiply that result by the derivative of what the expression is actually in terms of (in this case the derivative of 2x).

Let’s call the function in the argument of sec, g(x), which means the function is in the form of sec(x), except it does not have x as the angle, instead it has another function of x (2x) as the angle

If:

g(x) = 2x

It follows that:

sec(2x) = sec(g(x))

So if the function f(x) = sec(x) and the function g(x) = 2x, then the function sec(2x) can be written as a composite function.

f(x) = sec(x)

f(g(x)) = sec(g(x)) (but g(x) = 2x))

f(g(x)) = sec(2x)

Let’s define this composite function as F(x):

F(x) = f(g(x)) = sec(2x)

We can find the derivative of sec(2x) (F'(x)) by making use of the chain rule.

---

The Chain Rule:
For two differentiable functions f(x) and g(x)

If F(x) = f(g(x))

Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)

---

Now we can just plug f(x) and g(x) into the chain rule. But before we do that, just a quick recap on the derivative of the sec function.

The derivative of sec(x) with respect to x is sec(x)tan(x)
The derivative of sec(z) with respect to z is sec(z)tan(z)

In a similar way, the derivative of sec(2x) with respect to 2x is sec(2x)tan(2x).

We will use this fact as part of the chain rule to find the derivative of sec(2x) with respect to x.

How to find the derivative of sec(2x) using the Chain Rule:

F'(x)	= f'(g(x)).g'(x)	Chain Rule Definition
	= f'(g(x))(2)	g(x) = 2x ⇒ g'(x) = 2
	= (sec(2x)tan(2x)).(2)	f(g(x)) = sec(2x) ⇒ f'(g(x)) = sec(2x)tan(2x)
	= 2sec(2x)tan(2x)

Using the chain rule, the derivative of sec(2x) is 2sec(2x)tan(2x)

---

Finally, just a note on syntax and notation: sec(2x) is sometimes written in the forms below (with the derivative as per the calculation above). Just be aware that not all of the forms below are mathematically correct.

sec2x	► Derivative of sec2x = 2sec(2x)tan(2x)
sec 2 x	► Derivative of sec 2 x = 2sec(2x)tan(2x)
sec 2x	► Derivative of sec 2x = 2sec(2x)tan(2x)
sec (2x)	► Derivative of sec (2x) = 2sec(2x)tan(2x)

The Second Derivative Of sec(2x)

To calculate the second derivative of a function, you just differentiate the first derivative.

From above, we found that the first derivative of sec(2x) = 2sec(2x)tan(2x). So to find the second derivative of sec(2x), we just need to differentiate 2sec(2x)tan(2x)

We can use the chain rule to find the derivative of 2sec(2x)tan(2x) and it gives us a result of 8sec³(2x) – 4sec(2x)

► The second derivative of sec(2x) is 8sec³(2x) – 4sec(2x)

---

The derivative of cos^3x is -3cos²(x)sin(x)

---

How to calculate the derivative of cos^3x

Note that in this post we will be looking at differentiating cos³(x) which is not the same as differentiating cos(3x). Here is our post dealing with how to differentiate cos(3x).

The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.

In this case:

• We know how to differentiate cos(x) (the answer is -sin(x))
• We know how to differentiate x³ (the answer is 3x²)

This means the chain rule will allow us to perform the differentiation of the expression cos³(x).

Using the chain rule to find the derivative of cos^3x

Although the expression cos³x contains no parenthesis, we can still view it as a composite function (a function of a function).

We can write cos³x as (cos(x))³.

Now the function is in the form of x³, except it does not have x as the base, instead it has another function of x (cos(x)) as the base.

Let’s call the function of the base g(x), which means:

g(x) = cos(x)

From this it follows that:

cos(x)³ = g(x)³

So if the function f(x) = x³ and the function g(x) = cos(x), then the function (cos(x))³ can be written as a composite function.

f(x) = x³

f(g(x)) = g(x)³ (but g(x) = cos(x))

f(g(x)) = (cos(x))³

Let’s define this composite function as F(x):

F(x) = f(g(x)) = (cos(x))³

We can find the derivative of cos^3x (F'(x)) by making use of the chain rule.

---

The Chain Rule:
For two differentiable functions f(x) and g(x)

If F(x) = f(g(x))

Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)

---

Now we can just plug f(x) and g(x) into the chain rule.

How to find the derivative of cos^3x using the Chain Rule:

F'(x)	= f'(g(x)).g'(x)	Chain Rule Definition
	= f'(g(x))(-sin(x))	g(x) = cos(x) ⇒ g'(x) = sin(x)
	= (3cos2(x)).(-sin(x))	f(g(x)) = (cos(x))3 ⇒ f'(g(x)) = 3cos2(x)
	= -3cos2(x)sin(x)

Using the chain rule, the derivative of cos^3x is -3cos²(x)sin(x)

---

Finally, just a note on syntax and notation: cos^3x is sometimes written in the forms below (with the derivative as per the calculations above). Just be aware that not all of the forms below are mathematically correct.

cos3x	► Derivative of cos3x = -3cos2(x)sin(x)
cos^3(x)	► Derivative of cos^3(x) = -3cos2(x)sin(x)
cos 3 x	► Derivative of cos 3 x = -3cos2(x)sin(x)
(cosx)^3	► Derivative of (cosx)^3 = -3cos2(x)sin(x)
cos cubed x	► Derivative of cos cubed x = -3cos2(x)sin(x)
cos x cubed	► Derivative of cos x cubed = -3cos2(x)sin(x)
cosx3	► Derivative of cosx3 = -3cos2(x)sin(x)
cos^3	► Derivative of cos^3 = -3cos2(x)sin(x)

The Second Derivative Of cos^3x

To calculate the second derivative of a function, you just differentiate the first derivative.

From above, we found that the first derivative of cos^3x = -3cos²(x)sin(x). So to find the second derivative of cos^3x, we just need to differentiate -3cos²(x)sin(x).

We can use the product rule and trig identities to find the derivative of -3cos²(x)sin(x) and we get an answer of -3cos³(x) + 3sin(x)sin(2x)

► The second derivative of cos^3x is -3cos³(x) + 3sin(x)sin(2x)

---

The derivative of sin^3(x) is 3sin^2(x)cos(x)

---

How to calculate the derivative of sin^3x

Note that in this post we will be looking at differentiating sin³(x) which is not the same as differentiating sin(3x). Here is our post dealing with how to differentiate sin(3x).

The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.

In this case:

• We know how to differentiate sin(x) (the answer is cos(x))
• We know how to differentiate x³ (the answer is 3x²)

This means the chain rule will allow us to perform the differentiation of the expression sin^3(x).

Using the chain rule to find the derivative of sin^3(x)

Although the expression sin³x contains no parenthesis, we can still view it as a composite function (a function of a function).

We can write sin³x as (sin(x))³.

Now the function is in the form of x³, except it does not have x as the base, instead it has another function of x (sin(x)) as the base.

Let’s call the function of the base g(x), which means:

g(x) = sin(x)

From this it follows that:

sin(x)³ = g(x)³

So if the function f(x) = x³ and the function g(x) = sin(x), then the function (sin(x))³ can be written as a composite function.

f(x) = x³

f(g(x)) = g(x)³ (but g(x) = sin(x))

f(g(x)) = (sin(x))³

Let’s define this composite function as F(x):

F(x) = f(g(x)) = (sin(x))³

We can find the derivative of sin^3x (F'(x)) by making use of the chain rule.

---

The Chain Rule:
For two differentiable functions f(x) and g(x)

If F(x) = f(g(x))

Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)

---

Now we can just plug f(x) and g(x) into the chain rule.

How to find the derivative of sin^3(x) using the Chain Rule:

F'(x)	= f'(g(x)).g'(x)	Chain Rule Definition
	= f'(g(x))(cos(x))	g(x) = sin(x) ⇒ g'(x) = cos(x)
	= (3sin2(x)).(cos(x))	f(g(x)) = (sin(x))3 ⇒ f'(g(x)) = 3sin2(x)
	= 3sin2(x)cos(x)

Using the chain rule, the derivative of sin^3(x) is 3sin²(x)cos(x)

---

Finally, just a note on syntax and notation: sin^3(x) is sometimes written in the forms below (with the derivative as per the calculations above). Just be aware that not all of the forms below are mathematically correct.

sin3x	► Derivative of sin3x = 3sin2(x)cos(x)
sin^3x	► Derivative of sin^3x = 3sin2(x)cos(x)
sin 3 x	► Derivative of sin 3 x = 3sin2(x)cos(x)
(sinx)^3	► Derivative of (sinx)^3 = 3sin2(x)cos(x)
sin cubed x	► Derivative of sin cubed x = 3sin2(x)cos(x)
sin x cubed	► Derivative of sin x cubed = 3sin2(x)cos(x)
sinx3	► Derivative of sinx3 = 3sin2(x)cos(x)
sin^3	► Derivative of sin^3 = 3sin2(x)cos(x)

The Second Derivative Of sin^3(x)

To calculate the second derivative of a function, you just differentiate the first derivative.

From above, we found that the first derivative of sin^3x = 3sin²(x)cos(x). So to find the second derivative of sin^2x, we just need to differentiate 3sin²(x)cos(x).

We can use the product rule and trig identities to find the derivative of 3sin²(x)cos(x). We get an answer of -3sin³x + 3cos(x)sin(2x)

► The second derivative of sin^3(x) is -3sin³x + 3cos(x)sin(2x)

---

The derivative of cos(3x) is -3sin(3x)

---

How to calculate the derivative of cos(3x)

Note that in this post we will be looking at differentiating cos(3x) which is not the same as differentiating cos³x). Here is our post dealing with how to differentiate cos³(x).

The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.

In this case:

• We know how to differentiate cos(x) (the answer is -sin(x))
• We know how to differentiate 3x (the answer is 3)

This means the chain rule will allow us to differentiate the expression cos(3x).

Using the chain rule to find the derivative of cos(3x)

To perform the differentiation cos(3x), the chain rule says we must differentiate the expression as if it were just in terms of x as long as we then multiply that result by the derivative of what the expression is actually in terms of (in this case the derivative of 3x).

Let’s call the function in the argument of cos, g(x), which means the function is in the form of cos(x), except it does not have x as the angle, instead it has another function of x (3x) as the angle

If:

g(x) = 3x

It follows that:

cos(3x) = cos(g(x))

So if the function f(x) = cos(x) and the function g(x) = 3x, then the function cos(3x) can be written as a composite function.

f(x) = cos(x)

f(g(x)) = cos(g(x)) (but g(x) = 3x))

f(g(x)) = cos(3x)

Let’s define this composite function as F(x):

F(x) = f(g(x)) = cos(3x)

We can find the derivative of cos(3x) (F'(x)) by making use of the chain rule.

---

The Chain Rule:
For two differentiable functions f(x) and g(x)

If F(x) = f(g(x))

Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)

---

Now we can just plug f(x) and g(x) into the chain rule. But before we do that, just a quick recap on the derivative of the cos function.

The derivative of cos(x) with respect to x is -sin(x)
The derivative of cos(z) with respect to z is -sin(z)

In a similar way, the derivative of cos(3x) with respect to 3x is -sin(3x).

We will use this fact as part of the chain rule to find the derivative of cos(3x) with respect to x.

How to find the derivative of cos(3x) using the Chain Rule:

F'(x)	= f'(g(x)).g'(x)	Chain Rule Definition
	= f'(g(x))(3)	g(x) = 3x ⇒ g‘(x) = 3
	= (-sin(3x)).(3)	f(g(x)) = cos(3x) ⇒ f'(g(x)) = -sin(3x)
	= -3sin(3x)

Using the chain rule, the derivative of cos(3x) is -3sin(3x)

---

Finally, just a note on syntax and notation: cos(3x) is sometimes written in the forms below (with the derivative as per the calculation above). Just be aware that not all of the forms below are mathematically correct.

cos3x	► Derivative of cos3x = -3sin(3x)
cos 3 x	► Derivative of cos 3 x = -3sin(3x)
cos 3x	► Derivative of cos 3x = -3sin(3x)
cos (3x)	► Derivative of cos (3x) = -3sin(3x)

The Second Derivative Of cos(3x)

To calculate the second derivative of a function, you just differentiate the first derivative.

From above, we found that the first derivative of cos(3x) = -3sin(3x). So to find the second derivative of cos(3x), we just need to differentiate -3sin(3x)

We can use the chain rule to find the derivative of -3sin(3x) and it gives us a result of -9cos(3x)

► The second derivative of cos(3x) is -9cos(3x)

---

The derivative of sin(3x) is 3cos(3x)

---

How to calculate the derivative of sin(3x)

Note that in this post we will be looking at differentiating sin(3x) which is not the same as differentiating sin³(x). Here is our post dealing with how to differentiate sin³(x).

The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.

In this case:

• We know how to differentiate sin(x) (the answer is cos(x))
• We know how to differentiate 3x (the answer is 3)

This means the chain rule will allow us to differentiate the expression sin(3x).

Using the chain rule to find the derivative of sin(3x)

To perform the differentiation sin(3x), the chain rule says we must differentiate the expression as if it were just in terms of x as long as we then multiply that result by the derivative of what the expression is actually in terms of (in this case the derivative of 3x).

Let’s call the function in the argument of sin, g(x), which means the function is in the form of sin(x), except it does not have x as the angle, instead it has another function of x (3x) as the angle.

If:

g(x) = 3x

It follows that:

sin(3x) = sin(g(x))

So if the function f(x) = sin(x) and the function g(x) = 3x, then the function sin(3x) can be written as a composite function.

f(x) = sin(x)

f(g(x)) = sin(g(x)) (but g(x) = 3x))

f(g(x)) = sin(3x)

Let’s define this composite function as F(x):

F(x) = f(g(x)) = sin(3x)

We can find the derivative of sin(3x) (F'(x)) by making use of the chain rule.

---

The Chain Rule:
For two differentiable functions f(x) and g(x)

If F(x) = f(g(x))

Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)

---

Now we can just plug f(x) and g(x) into the chain rule. But before we do that, just a quick recap on the derivative of the sin function.

The derivative of sin(x) with respect to x is cos(x)
The derivative of sin(z) with respect to z is cos(z)

In a similar way, the derivative of sin(3x) with respect to 3x is cos(3x).

We will use this fact as part of the chain rule to find the derivative of sin(3x) with respect to x.

How to find the derivative of sin(3x) using the Chain Rule:

F'(x)	= f'(g(x)).g'(x)	Chain Rule Definition
	= f'(g(x))(3)	g(x) = 3x ⇒ g'(x) = 3
	= (cos(3x)).(3)	f(g(x)) = sin(3x) ⇒ f'(g(x)) = cos(3x)
	= 3cos(3x)

Using the chain rule, the derivative of sin(3x) is 3cos(3x)

---

Finally, just a note on syntax and notation: sin(3x) is sometimes written in the forms below (with the derivative as per the calculation above). Just be aware that not all of the forms below are mathematically correct.

sin3x	► Derivative of sin3x = 3cos(3x)
sin3x	► Derivative of sin3x = 3cos(3x)
sin 3x	► Derivative of sin 3x = 3cos(3x)
sin (3x)	► Derivative of sin (3x) = 3cos(3x)

The Second Derivative Of sin(3x)

To calculate the second derivative of a function, you just differentiate the first derivative.

From above, we found that the first derivative of sin(3x) = 3cos(3x). So to find the second derivative of sin(3x), we just need to differentiate 3cos(3x)

We can use the chain rule to find the derivative of 3cos(3x) and it gives us a result of -9sin(3x)

► The second derivative of sin(3x) is -9sin(3x)