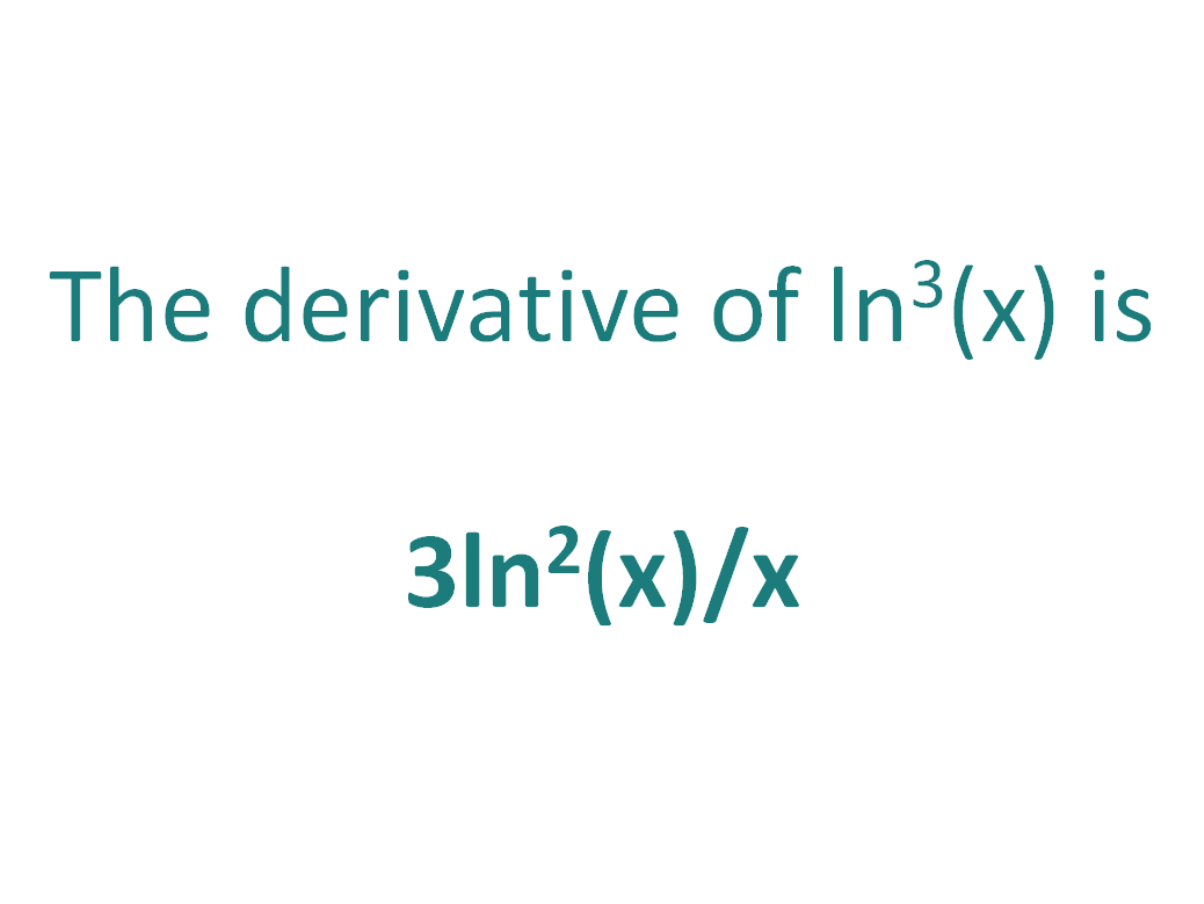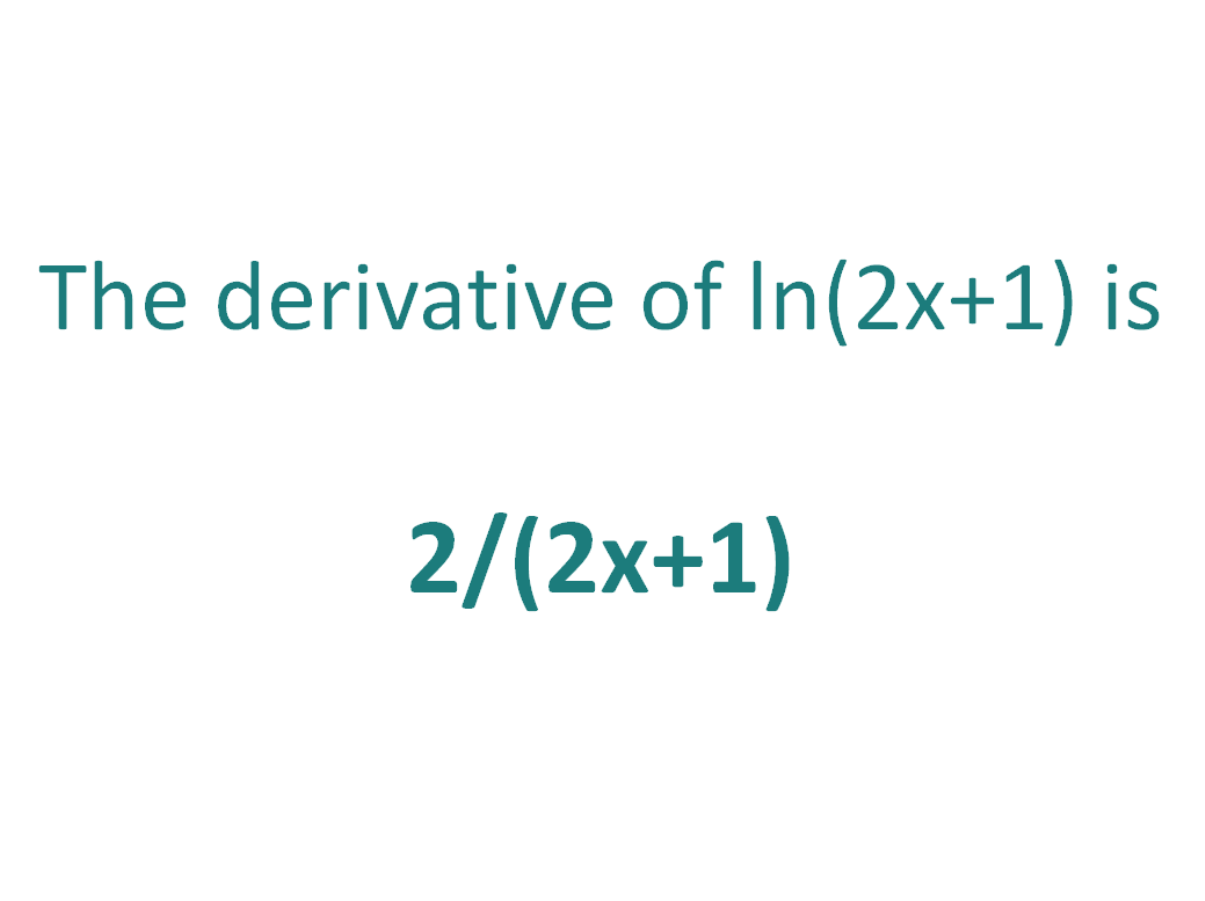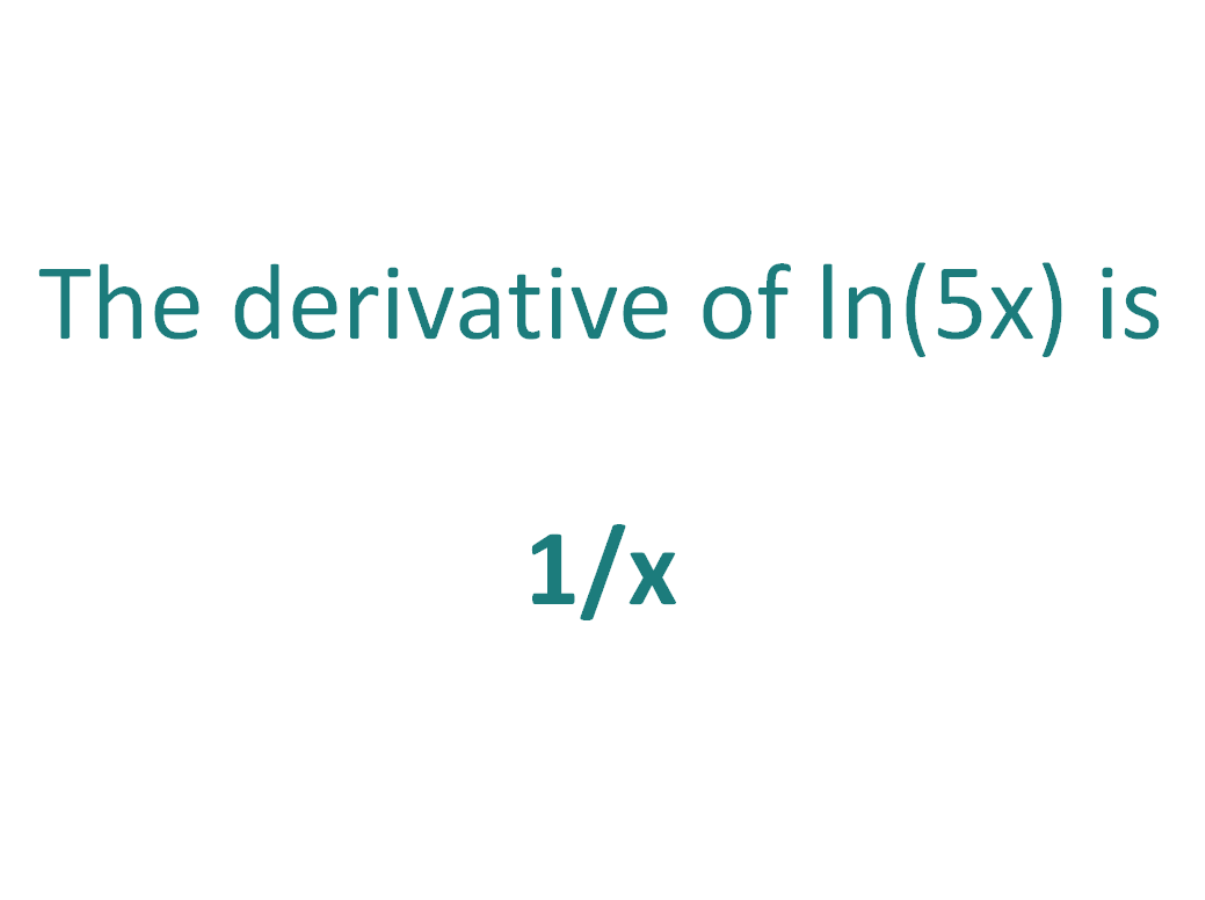The derivative of ln^3(x) is 3ln2(x)/x
How to calculate the derivative of ln^3(x)
Note that in this post we will be looking at differentiating ln3(x) which is not the same as differentiating ln(3x). Here is our post dealing with how to differentiate ln(3x)
The chain rule is useful for finding the derivative of a function which could have been differentiated had it been in x, but it is in the form of another expression which could also be differentiated if it stood on its own.
In this case:
- We know how to differentiate ln(x) (the answer is l/x)
- We know how to differentiate x3 (the answer is 3x2)
This means the chain rule will allow us to perform the differentiation of the expression ln^3x.
Using the chain rule to find the derivative of ln^3x
Although the expression ln3x contains no parenthesis, we can still view it as a composite function (a function of a function).
We can write ln3x as (ln(x))3.
Now the function is in the form of x3, except it does not have x as the base, instead it has another function of x (ln(x)) as the base.
Let’s call the function of the base g(x), which means:
g(x) = ln(x)
From this it follows that:
(ln(x))3 = g(x)3
So if the function f(x) = x3 and the function g(x) = ln(x), then the function (ln(x))3 can be written as a composite function.
f(x) = x3
f(g(x)) = g(x)3 (but g(x) = ln(x))
f(g(x)) = (ln(x))3
Let’s define this composite function as F(x):
F(x) = f(g(x)) = (ln(x))3
We can find the derivative of ln^3x (F'(x)) by making use of the chain rule.
The Chain Rule:
For two differentiable functions f(x) and g(x)
If F(x) = f(g(x))
Then the derivative of F(x) is F'(x) = f’(g(x)).g’(x)
Now we can just plug f(x) and g(x) into the chain rule.
How to find the derivative of ln^3x using the Chain Rule:
| F'(x) | = f'(g(x)).g'(x) | Chain Rule Definition |
| = f'(g(x))(1/x) | g(x) = ln(x) ⇒ g'(x) = 1/x | |
| = (3ln2(x)).(1/x)) | f(g(x)) = (ln(x))3 ⇒ f'(g(x)) = 3ln2(x) | |
| = 3ln2(x)/x |
Using the chain rule, the derivative of ln^3x is 3ln^2(x)/x
Finally, just a note on syntax and notation: ln^3x is sometimes written in the forms below (with the derivative as per the calculations above). Just be aware that not all of the forms below are mathematically correct.
| ln3x | ► Derivative of ln3x = 3ln2(x)/x |
| ln^3x | ► Derivative of ln^3x = 3ln2(x)/x |
| ln 3 x | ► Derivative of ln 3 x = 3ln2(x)/x |
| (lnx)^3 | ► Derivative of (lnx)^3 = 3ln2(x)/x |
| ln cubed x | ► Derivative of ln cubed x = 3ln2(x)/x |
| lnx3 | ► Derivative of lnx3 = 3ln2(x)/x |
| ln^3 | ► Derivative of ln^3 = 3ln2(x)/x |
The Second Derivative Of ln^3x
To calculate the second derivative of a function, you just differentiate the first derivative.
From above, we found that the first derivative of ln^3x = 3ln2(x)/x. So to find the second derivative of ln^3x, we just need to differentiate 3ln2(x)/x
We can use a combination of the chain rule and the quotient rule to find the derivative of 3ln2(x)/x.
We can set f(x) = ln2(x) and g(x) = x and apply the quotient rule (and the chain rule on f(x)) to find the derivative of f(x)/g(x) = 3(-ln2(x) + 2ln(x))/x2
► The second derivative of ln^3x is 3(-ln2(x) + 2ln(x))/x2